数据结构之trie树
[toc]
数据结构之Trie树
Trie定义
Trie 树,也叫「前缀树」或「字典树」,顾名思义,它是一个树形结构,专门用于处理字符串匹配,用来解决在一组字符串集合中快速查找某个字符串的问题。
Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起,比如我们有["hello","her","hi","how","see","so"] 这个字符串集合,可以将其构建成下面这棵 Trie 树:
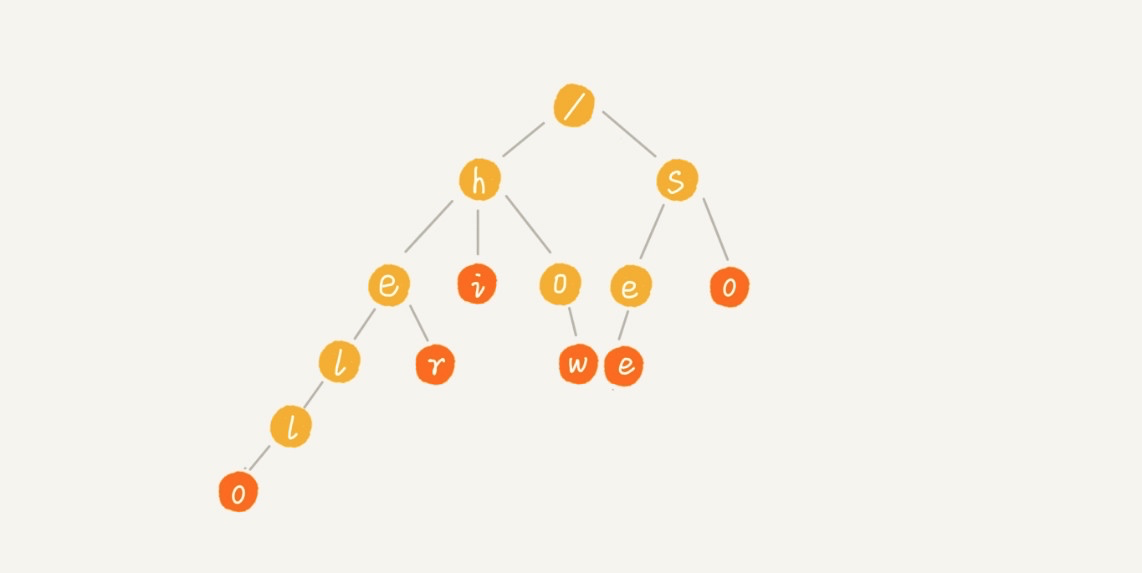
每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(红色节点表示是某个单词的结束字符,但不一定都是叶子节点)。
这样,我们就可以通过遍历这棵树来检索是否存在待匹配的字符串了,比如我们要在这棵 Trie 树中查询 her,只需从 h 开始,依次往下匹配,在子节点中找到 e,然后继续匹配子节点,在 e 的子节点中找到 r,则表示匹配成功,否则匹配失败。通常,我们可以通过 Trie 树来构建敏感词或关键词匹配系统。
Trie 树的实现
从刚刚 Trie 树的介绍来看,Trie 树主要有两个操作,一个是将字符串集合构造成 Trie 树。这个过程分解开来的话,就是一个将字符串插入到 Trie 树的过程。另一个是在 Trie 树中查询一个字符串。
Trie 树是个多叉树,二叉树中,一个节点的左右子节点是通过两个指针来存储的,对于多叉树来说,我们怎么存储一个节点的所有子节点的指针呢?
我们将 Trie 树的每个节点抽象为一个节点对象,对象包含的属性有节点字符、子节点字典和是否是字符串结束字符标志位:
type Node struct {
children map[rune]*Node //孩子节点
char string //保存的字符
isEnding bool //记录是否为末节点
}
// 初始化一个节点
func NewNode(char string) *Node {
return &Node{
children: make(map[rune]*Node),
char: char,
isEnding: false,
}
}
要构造一棵完整的 Trie 树,关键在于存储子节点字典的 children 属性的实现。借助散列表的思想,我们通过一个下标与字符一一映射的数组,来构造 children:将字符串中每个字符转化为 Unicode 编码作为字典键,将对应节点对象指针作为字典值,依次插入所有字符串,从而构造出 Trie 树。对应 Go 实现代码如下:
//构造一棵树
type Trie struct {
root *Node
}
//初始化树
func NewTrie() *Trie {
return &Trie{
root: NewNode("/"),
}
}
// Insert 插入单词
func (trie *Trie) Insert(str string) {
curNode := trie.root
for _, ch := range str {
//查看当前是否存在对应字符的k-v对
value, ok := curNode.children[ch] //读当前节点的子节点
if !ok {
value = NewNode(string(ch))
curNode.children[ch] = value
}
//更新当前节点
curNode = value
}
//个单词遍历完所有字符后将结尾字符打上标记
curNode.isEnding = true
}
func (trie *Trie) Find(str string) bool {
curNode := trie.root
for _, ch := range str {
//查看当前是否存在对应字符的k-v对
value, ok := curNode.children[ch]
if !ok {
return false
}
//指向孩子节点
curNode = value
}
//判断是否为末节点
if curNode.isEnding == false {
return false
}
return true
}
func (trie *Trie) StartsWith(str string) bool {
curNode := trie.root
for _, ch := range str {
//查看当前是否存在对应字符的k-v对
value, ok := curNode.children[ch]
if !ok {
return false
}
curNode = value
}
return true
}
测试:
func main() {
trie := NewTrie()
trie.Insert("iceymoss")
trie.Insert("apple")
fmt.Println(trie.Find("iceymos"))
fmt.Println(trie.Find("apple"))
fmt.Println(trie.StartsWith("app"))
}
输出:
false
true
true
Trie 树的复杂度
构建 Trie 树的过程比较耗时,对于有 n 个字符的字符串集合而言,需要遍历所有字符,对应的时间复杂度是 O(n),但是一旦构建之后,查询效率很高,如果匹配串的长度是 k,那只需要匹配 k 次即可,与原来的主串没有关系,所以对应的时间复杂度是 O(k),基本上是个常量级的数字。
Trie 树显然也是一种空间换时间的做法,构建 Trie 树的过程需要额外的存储空间存储 Trie 树,而且这个额外的空间是原来的数倍。
Trie的应用场景
Trie 树适用于那些查找前缀匹配的字符串、比如敏感词过滤和搜索框联想功能、IDE 代码编辑器自动补全、输入法自动补全功能等。