数据结构之二分搜索树
[toc]
概念及其介绍
概念
二分搜索树(英语:Binary Search Tree),也称为 二叉查找树 、二叉搜索树 、有序二叉树或排序二叉树。满足以下几个条件:
- 每个节点的键值大于左孩子
- 每个节点的键值小于右孩子
- 以左右孩子为根的子数仍然为二分搜索树
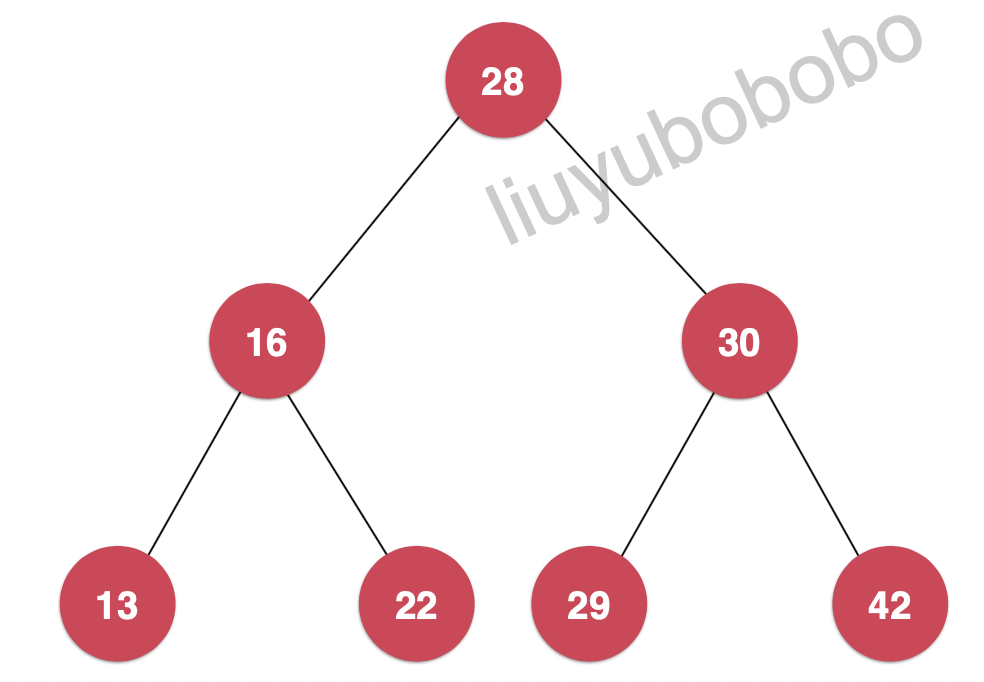
- 优点
可以高效的查找数据,还可以高效的插入,删除,及动态维护数据
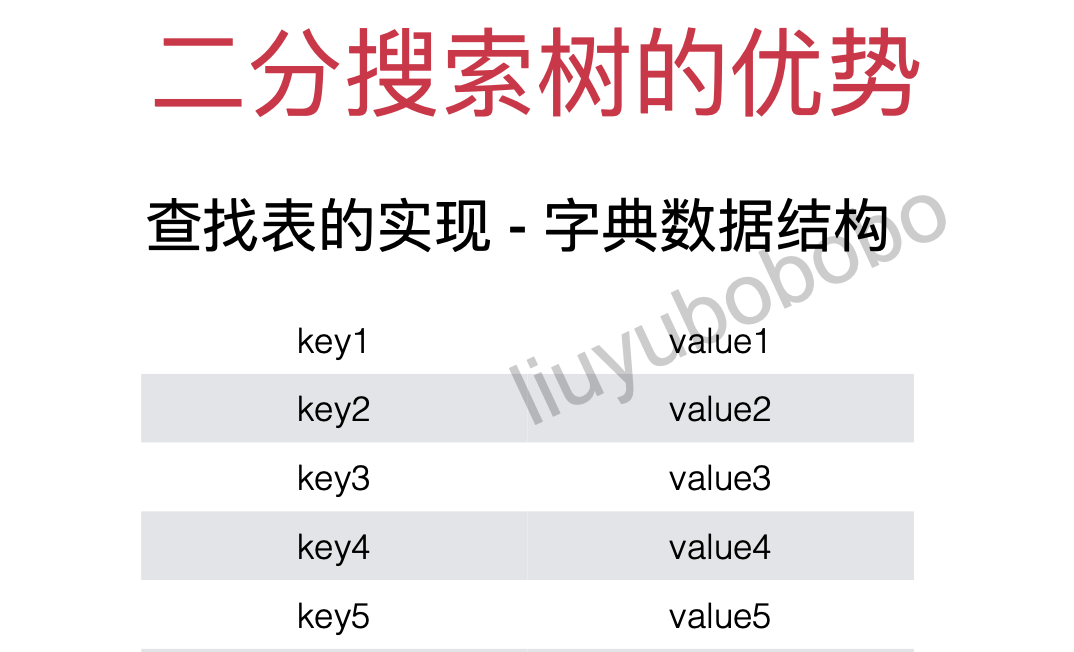
二分搜索树有着高效的插入、删除、查询操作。
平均时间的时间复杂度为 O(log n),最差情况为 O(n)。二分搜索树与堆不同,不一定是完全二叉树,底层不容易直接用数组表示故采用链表来实现二分搜索树。
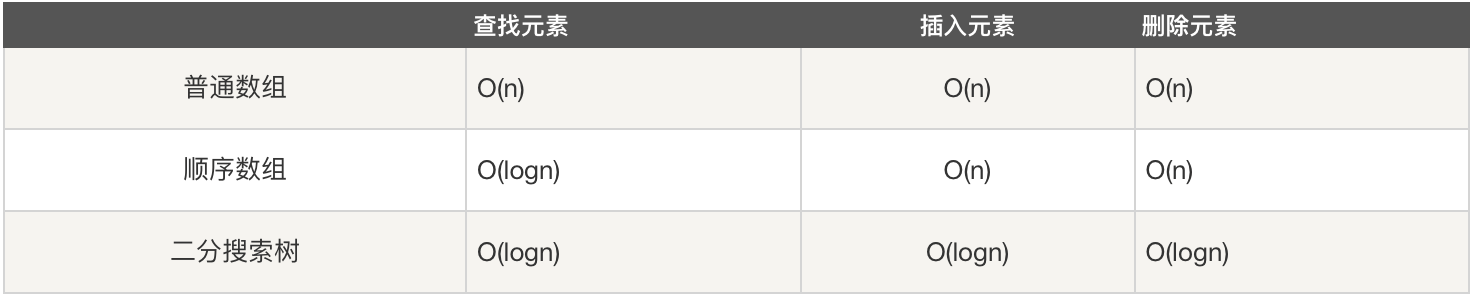
特性
顺序性
二分搜索树可以当做查找表的一种实现。
我们使用二分搜索树的目的是通过查找 key 马上得到 value。minimum、maximum、successor(后继)、predecessor(前驱)、floor(地板)、ceil(天花板、rank(排名第几的元素)、select(排名第n的元素是谁)这些都是二分搜索树顺序性的表现。
局限性
二分搜索树在时间性能上是具有局限性的。
如下图所示,元素节点一样,组成两种不同的二分搜索树,都是满足定义的:
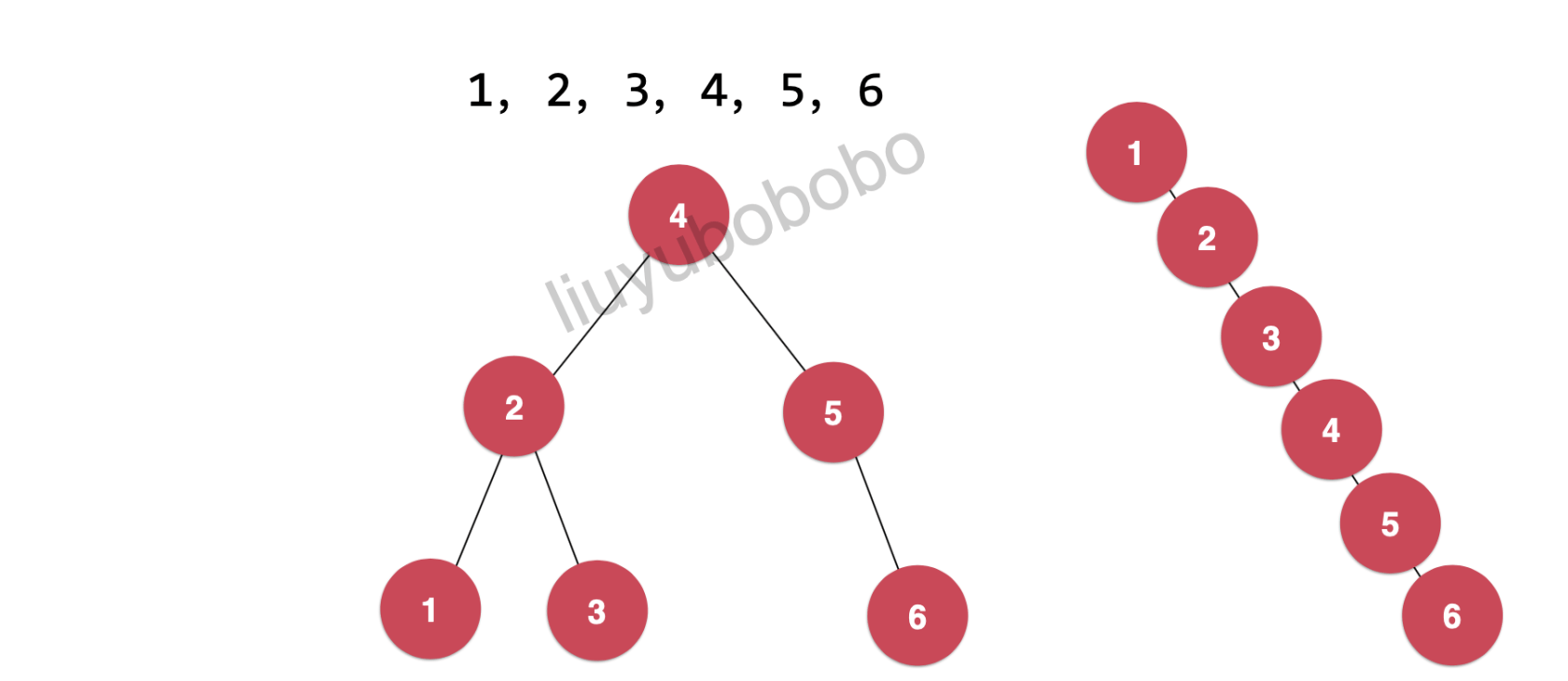
二叉搜索树可能退化成链表,相应的,二叉搜索树的查找操作是和这棵树的高度相关的,而此时这颗树的高度就是这颗树的节点数 n,同时二叉搜索树相应的算法全部退化成 O(n) 级别。
操作:二分搜索树
-
插入操作(insert)
-
数据的查找(Search)
-
二分搜索树的包含(Contain)
-
二分搜索树的遍历
-
二分搜索树节点删除
二分搜索树节点的插入
定义二分搜索树
首先定义一颗二分搜索树,C++代码如下:
#include <iostream>
#include <queue>
#include <cassert>
using namespace std;
//套用模板函数
template <typename Key, typename Value>
class BST {
private:
//构造节点Node
struct Node {
Key key;
Value value;
Node *left; //左孩子指针
Node *right; //右孩子指针
Node(Key key, Value value) {
this->key = key;
this->value = value;
//初始值为空
this->left = this->right = NULL;
}
Node(Node *node){
this->key = node->key;
this->value = node->value;
this->left = node->left;
this->right = node->right;
}
};
//根节点
Node *root;
//节点数量
int count;
public:
//构造函数
BST() {
//初始值为空
root = NULL;
count = 0;
}
//析构函数
~BST() {
distroy(root);
}
插入节点
接下来我们开始对二分搜索树中进行插入节点,如图:
我们向树中插入键值为60的节点
- 首先60会和整个数的根节点比较,显然60 > 41 所以将60,继续和41节点的右孩子进行比较:
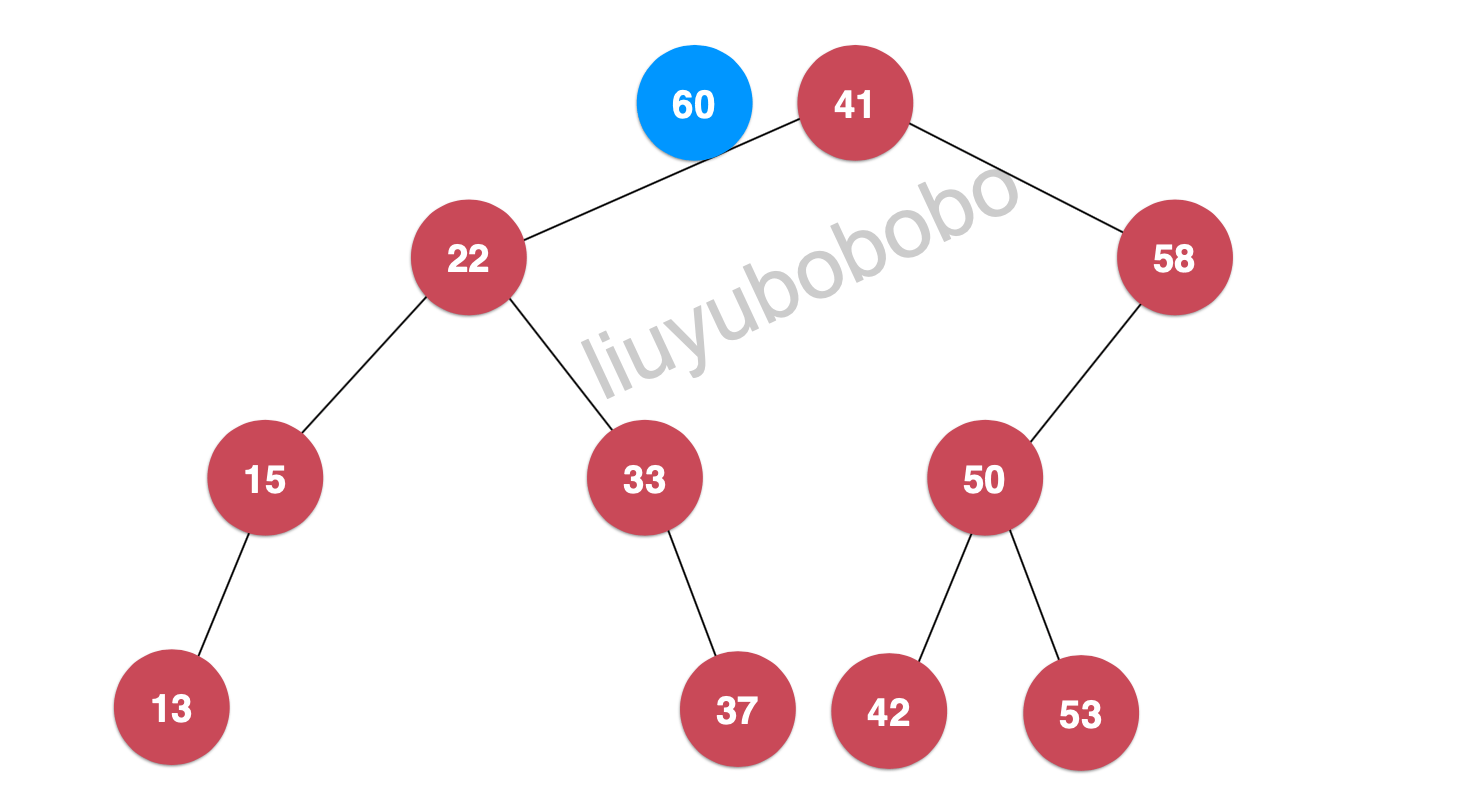
- 此时 60 > 58 ,所以将60 继续和58节点的右孩子节点进行比较,但58节点的右孩子为空,这时 60 节点就插入为58节点的右孩子:
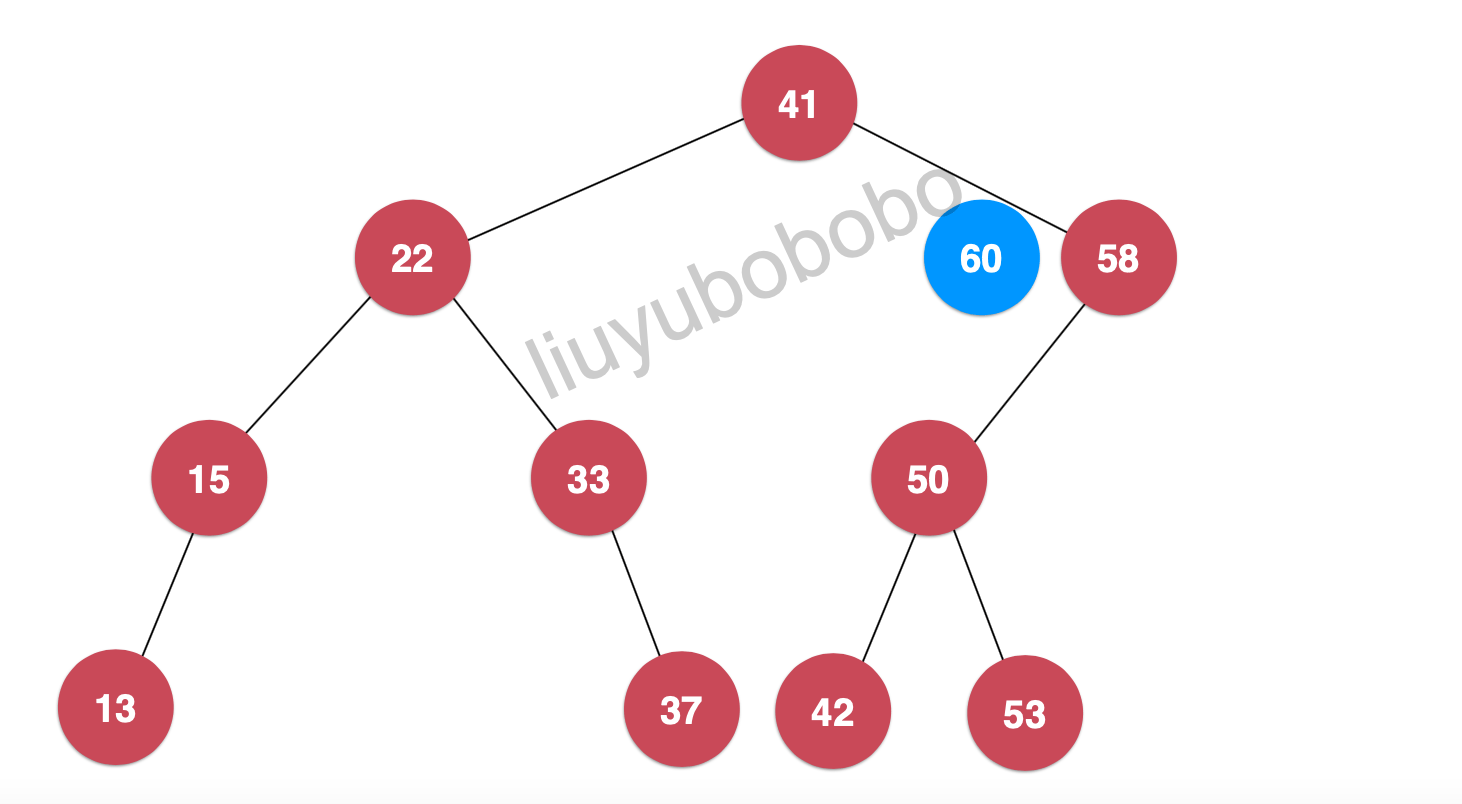
下面我们再向二分搜索树中插入键值为28的节点:
- 节点28和二分搜索树的根节点41比较,28 < 41 ,将28继续和41节点的左孩子节点比较:
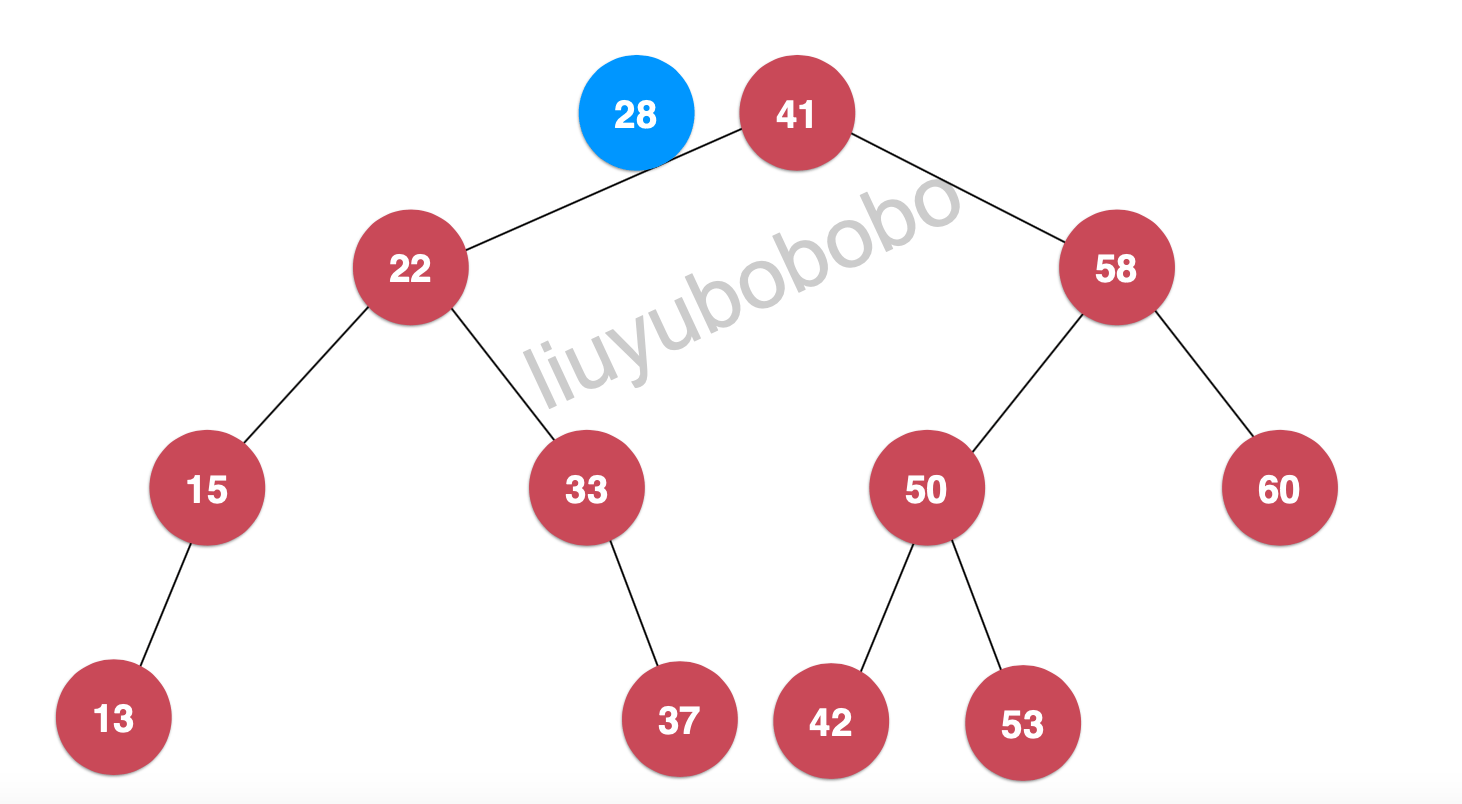
- 此时28 > 22, 再将28和22节点的左孩子比较:
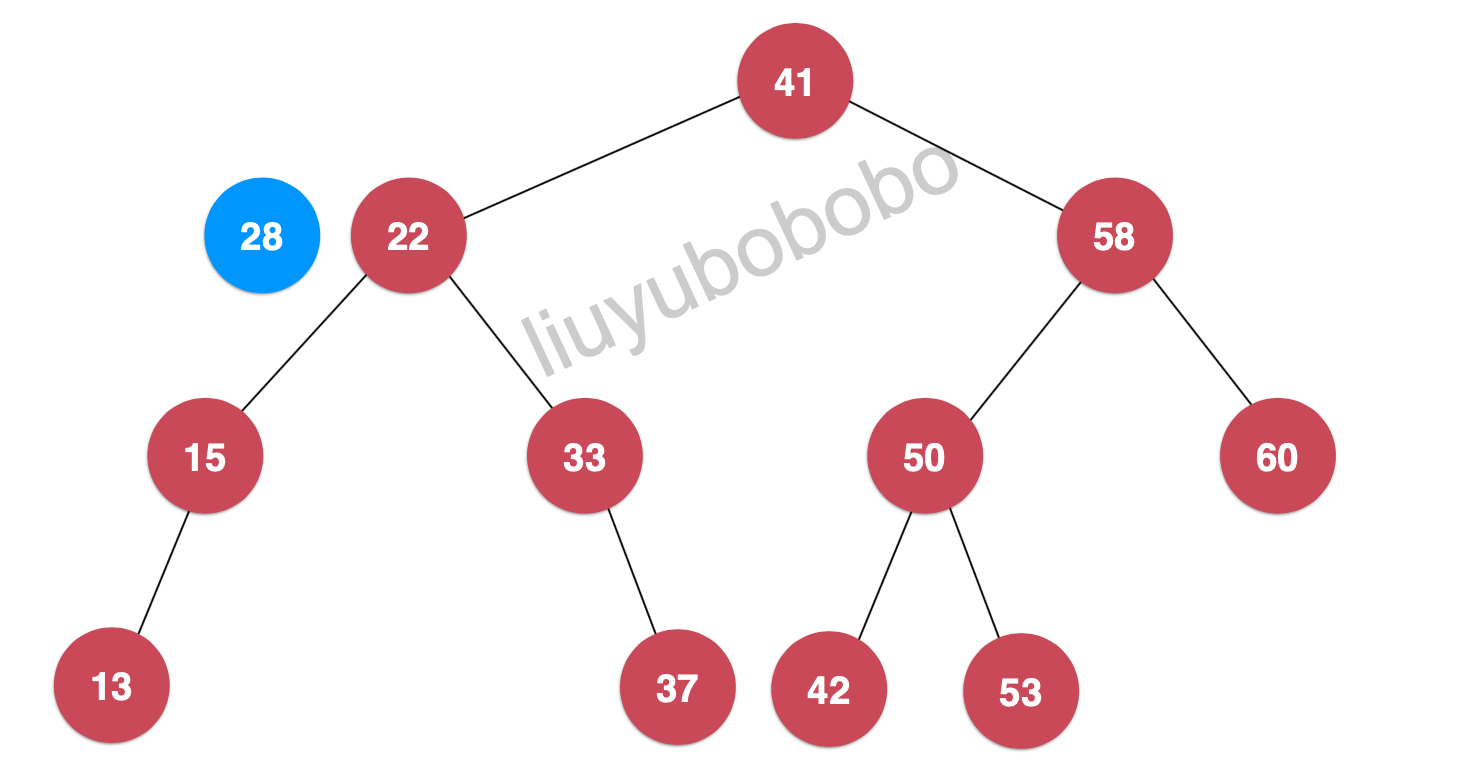
- 28 < 33,继续将节点28和33节点的右孩子比较,但此时33的左孩子为空,28节点就插入为节点33的左孩子:
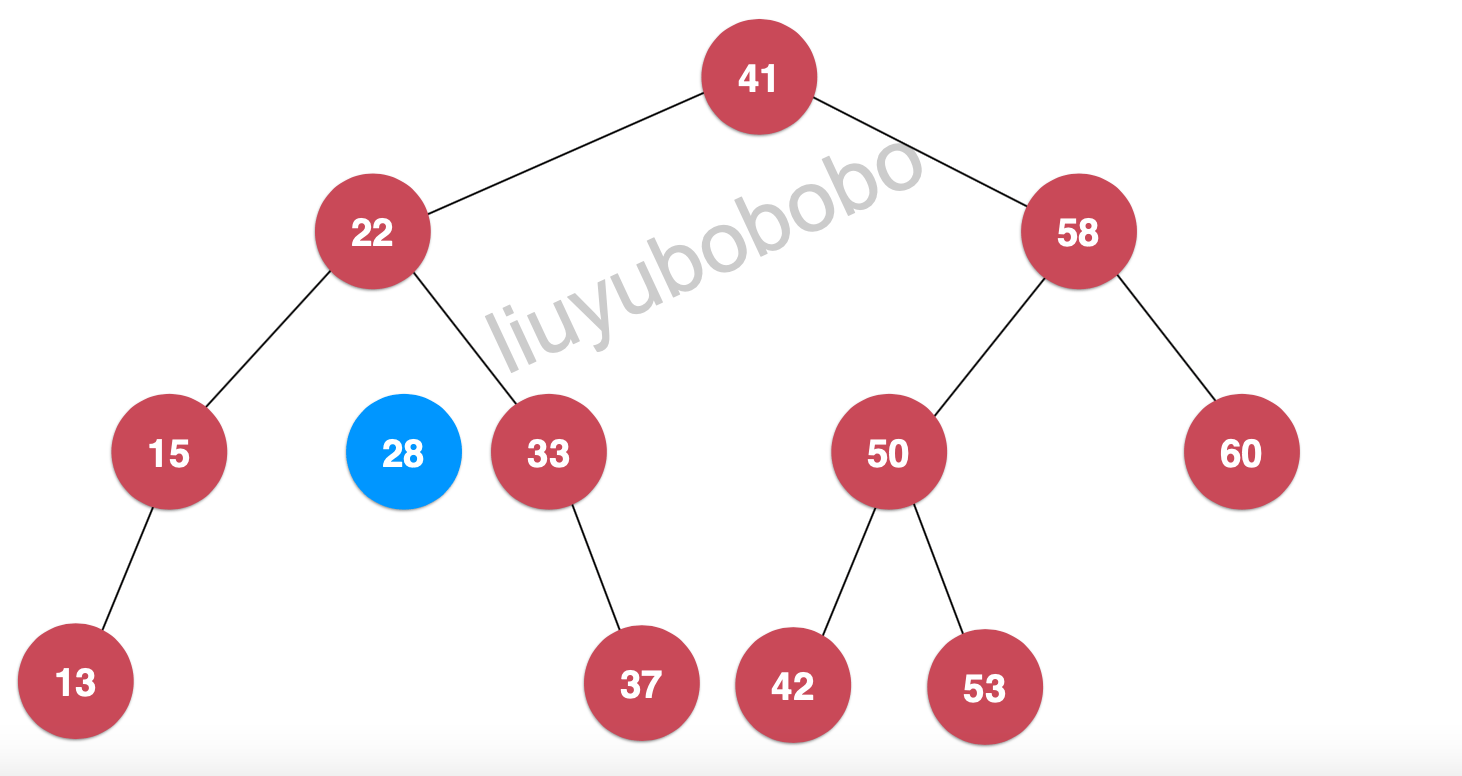
如果出现插入的节点和二分搜索树中的节点重合的情况,依然是同理,只需要将原来节点覆盖即可
代码实现
新节点的插入操作的逻辑明白了,下面我们开始带着这种逻辑进入代码的实现(使用递归版本,c++实现): 我们在public中定义函数:
//插入操作
void insert(Key key, Value value) {
//向根节点中插入key, value
root = insert(root, key, value);
}
接下来我们在private中写:
//插入操作
//向以node为根节点的二分搜索树中,插入节点(key,value),使用递归算法
//返回插入新节点后的二分搜索树的根
Node *insert(Node *node, Key key, Value value) {
if (node == NULL) {
count++;
return new Node(key, value);
}
if (key == node->key) {
node->value = value;
}
else if (key > node->key) {
node->right = insert(node->right, key, value);
}
else //key < node->key
node->left = insert(node->left, key, value);
}
二分搜索树之查找(Search)-包含(Contain)
查找(Search)
逻辑
前面我们了解了对节点的插入,其实在二分搜索树中对相应节点的查找的过程中也有同样的逻辑 下面我们来看看具体的查找(Search): 我们在树中查找键值为42的节点
-
将42和41比较,42 > 41,根据二分搜索树的定义可知,我们应该继续往41节点的右孩子查找:
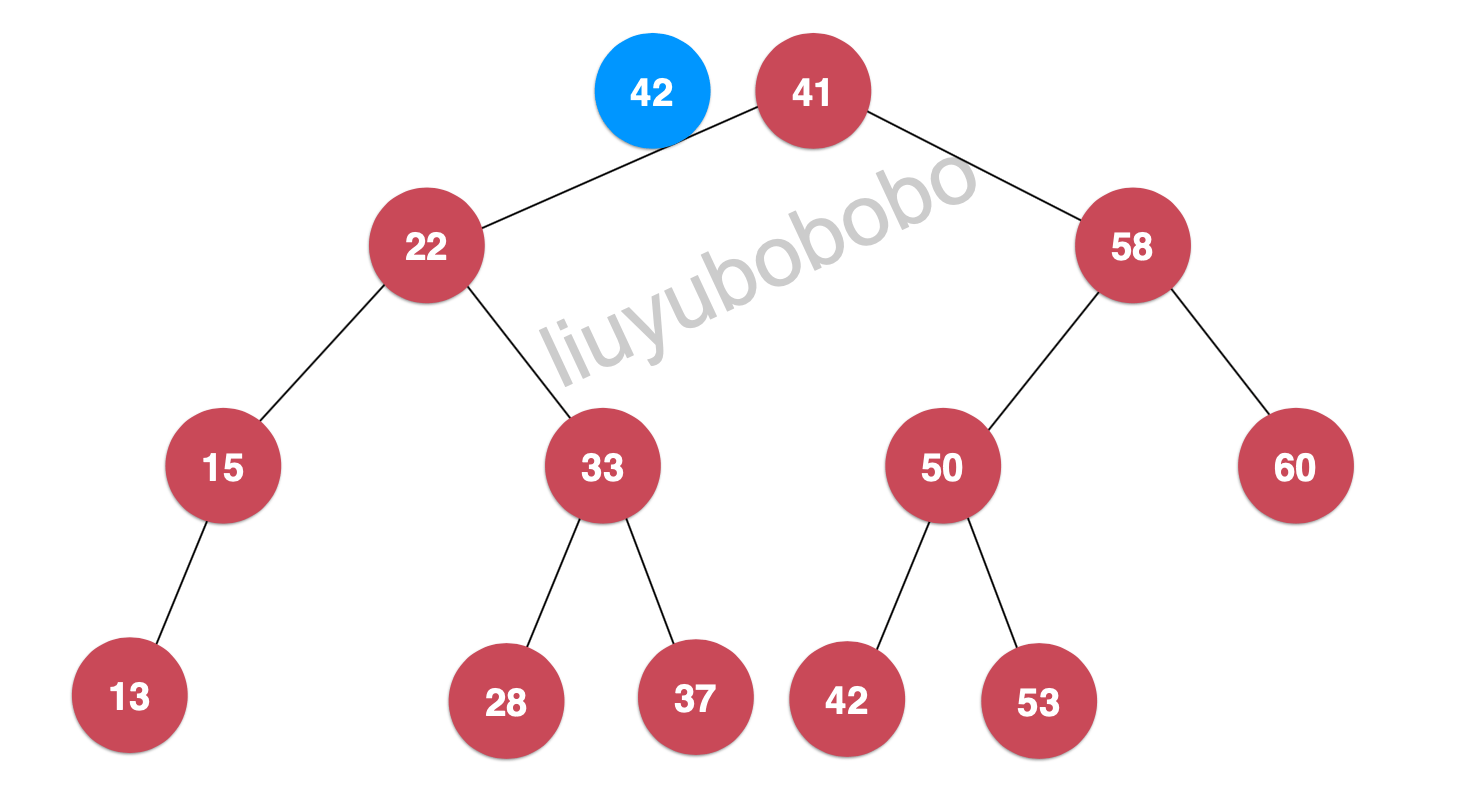
-
此时再将42和58比较,42 < 58,继续向58节点的左孩子节点查找
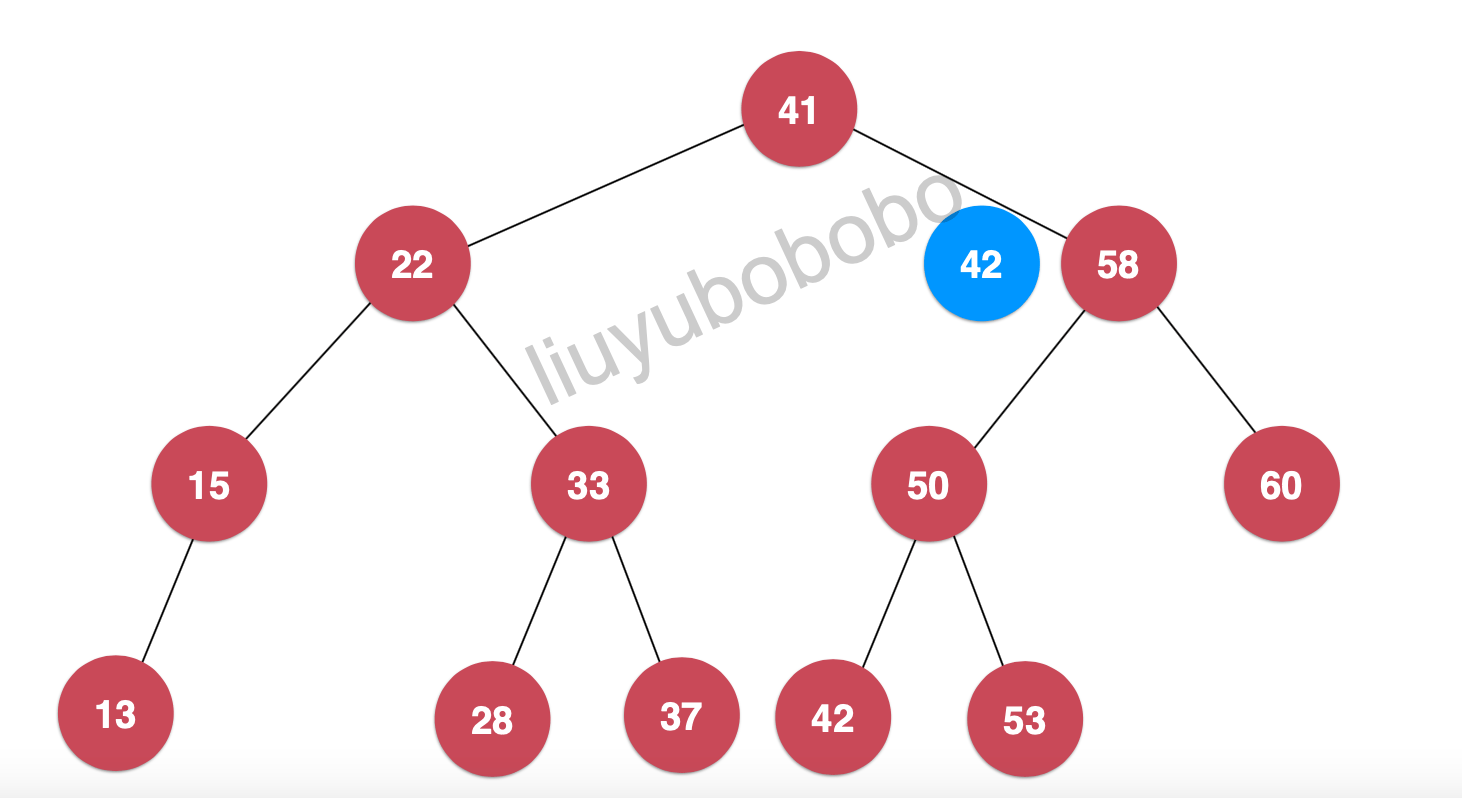
-
42 < 50,继续向50节点的左孩子查找,此时50节点的左孩子就为42,所以我们就找到了节点42,并返回对应的value值
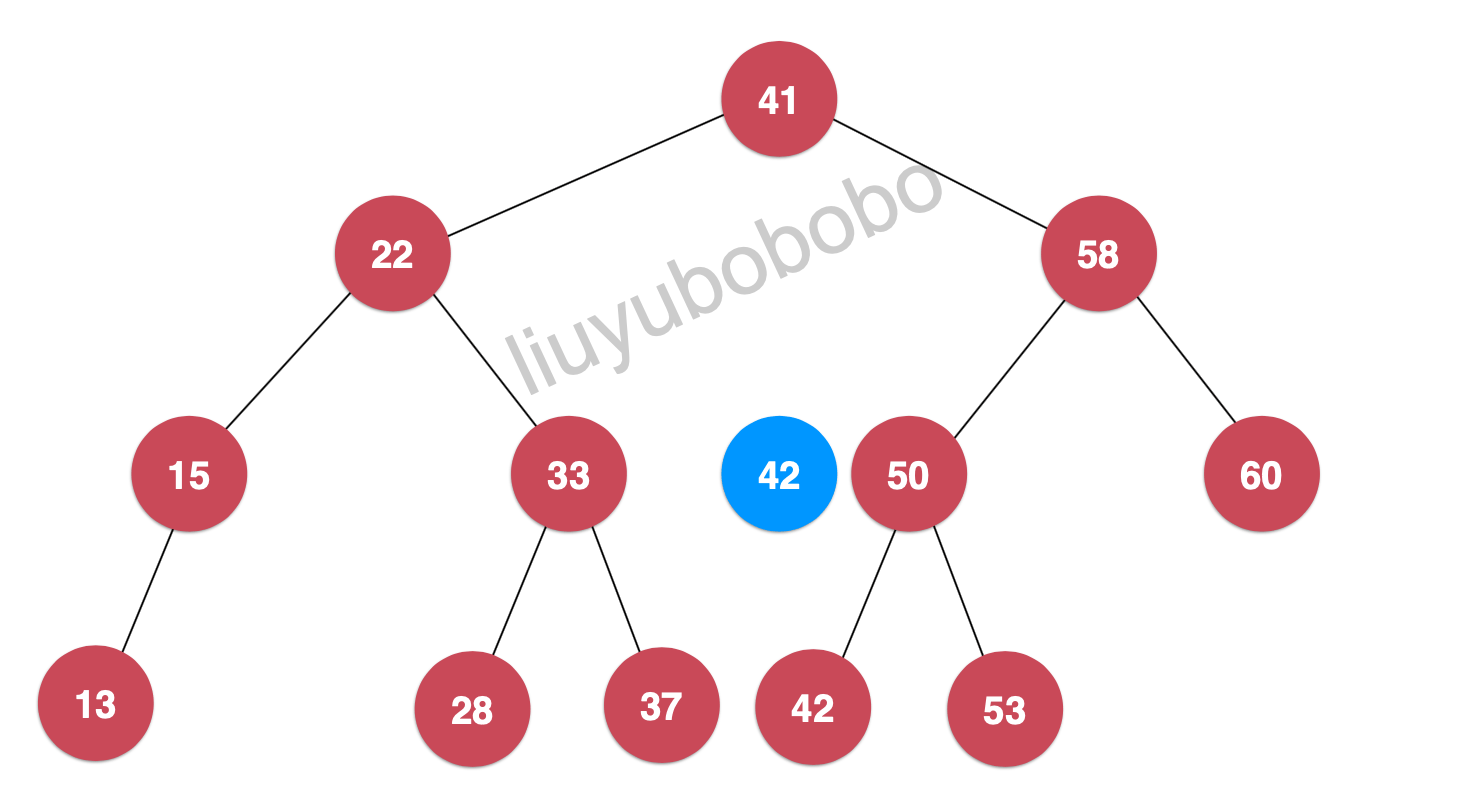
如果我们要查找的节点不存在,则返回空或false
代码实现(使用递归,c++实现)
在public中定义:
//找到key相应的节点并且返回value的地址
Node *seacher(Key key, Value value) {
return seacher(root, key, value);
}
在private中定义:
//在二分搜索树中找到相应元素并返回该元素的地址
Value *seacher(Node *node, Key key) {
if (key == NULL)
return NULL;
//找到key 返回value的地址
if (key == node->key)
return &(node->value);
else if (key > node->key)
return seacher(node->right, key);
else return seacher(node->left, key);
}
包含(Contain)
逻辑
前面我们将了"查找",其实"包含"的逻辑和"查找"是一样的,只是目的不同,“查找"的目的是找到我们需要找的节点并返回对应的地址; “包含(Contain)“的目的是判断二分搜索树中是否存在一个节点,如果存在则返回true,否则返回false。 其逻辑和操作过程和"查找(Search)“一样的
代码实现(使用递归,c++实现)
在public中定义:
//在树中寻找是否存在key
bool contain(Key key) {
return contain(root, key);
}
在private中定义:
//在二分搜索树中查找key,存在返回trun不存在返回false
bool contain(Node *node, Key key) {
//元素不存在
if (key == NULL)
return false;
//元素存在
if (key == node->key)
return true;
else if (key > node->key)
return contain(node->right, key);
else return contain(node->left, key);
}
二分搜索树的遍历
遍历的分类
二分搜索树遍历分为两大类,深度优先遍历和层序遍历。 深度优先遍历分为三种:先序遍历(preorder tree walk)、中序遍历(inorder tree walk)、后序遍历(postorder tree walk),分别为: 1、前序遍历:先访问当前节点,再依次递归访问左右子树。 2、中序遍历:先递归访问左子树,再访问自身,再递归访问右子树。 3、后序遍历:先递归访问左右子树,再访问自身节点。
深度优先遍历
- 前序遍历:先访问当前节点,再依次递归访问左右子树。
- 中序遍历:先递归访问左子树,再访问自身,再递归访问右子树。
- 后序遍历:先递归访问左右子树,再访问自身节点。 为了更好理解深度优先遍历我们使用下图模型:
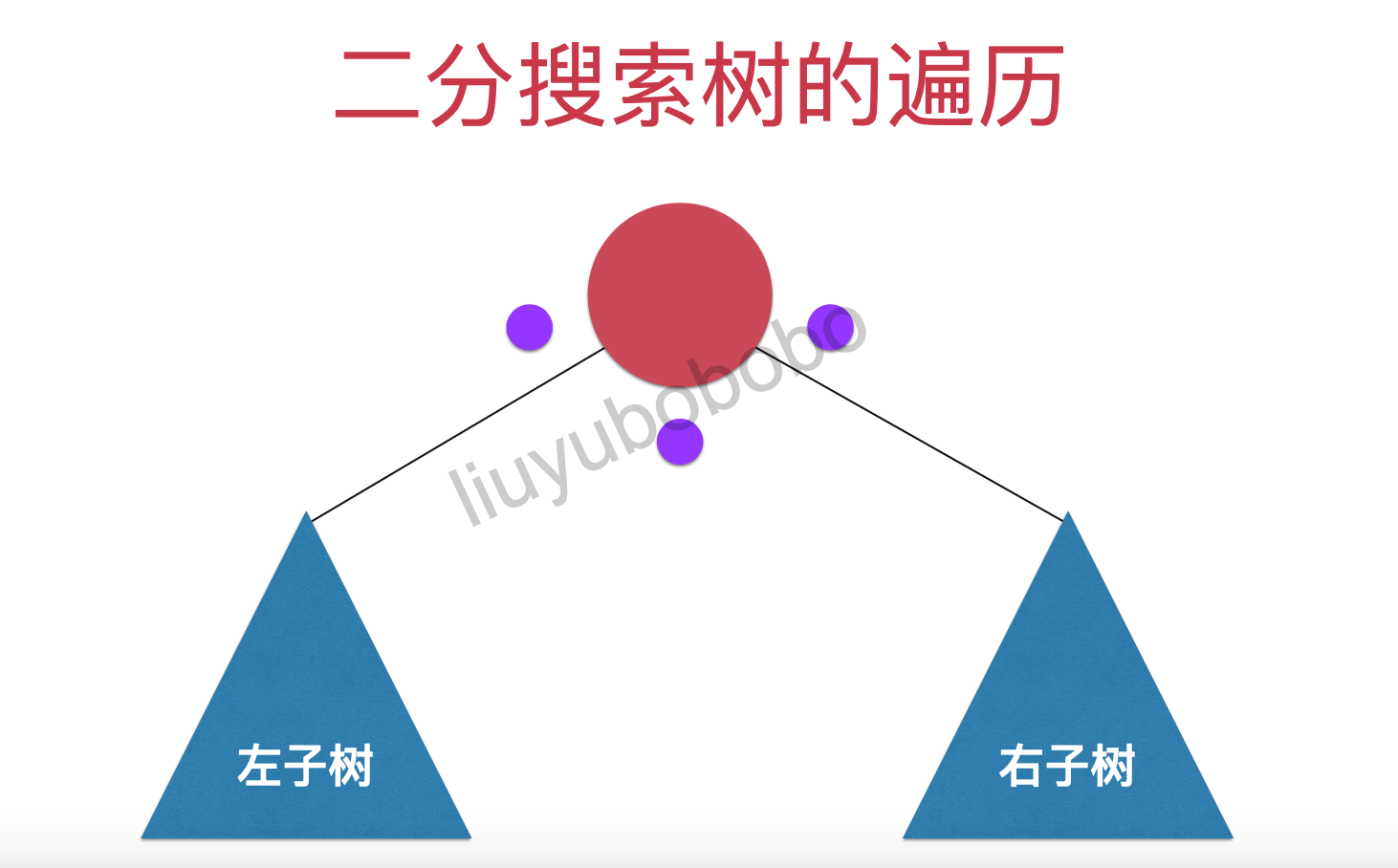
前序遍历:
我们对二分搜索树中所有节点都分别标记3个点:
 开始遍历:
前序遍历是对每一个节点第一次访问的时候进行遍历:
28
开始遍历:
前序遍历是对每一个节点第一次访问的时候进行遍历:
28
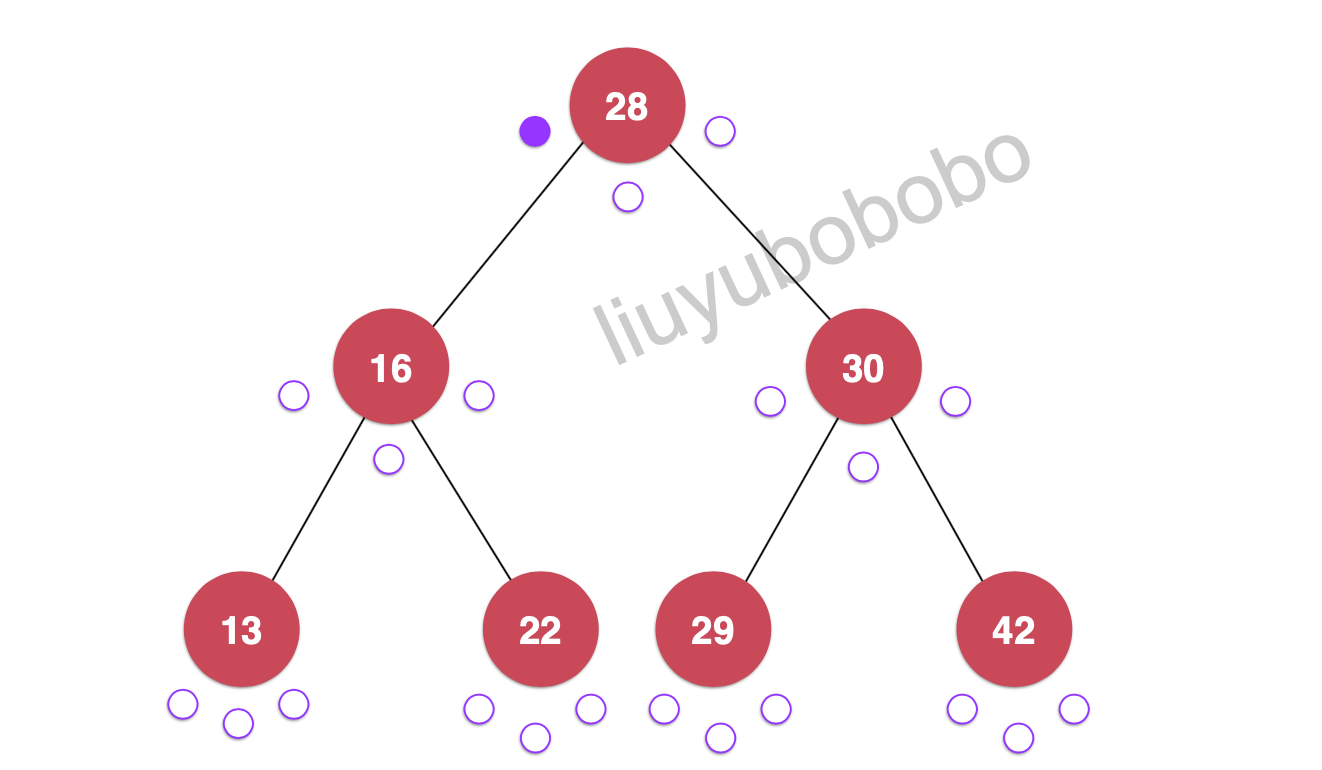 遍历:28, 16
遍历:28, 16
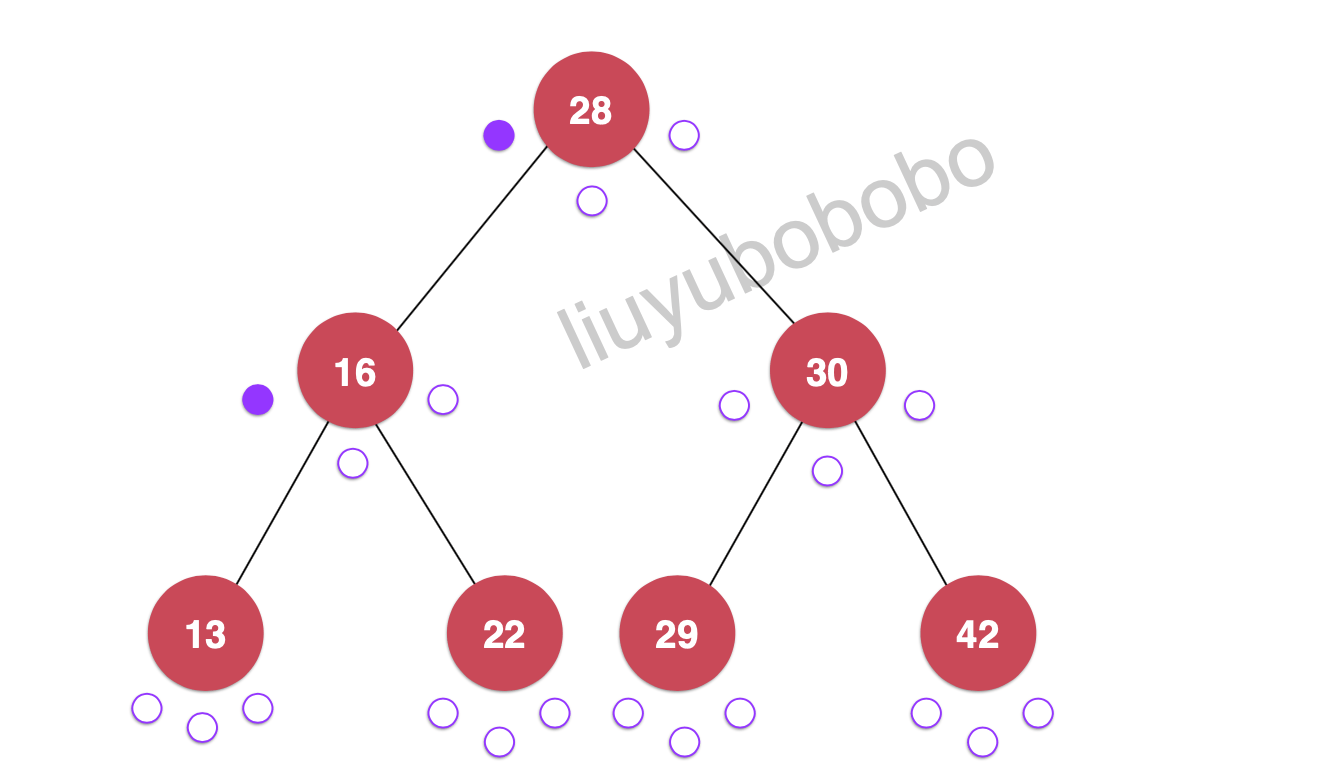
遍历:28, 16, 13
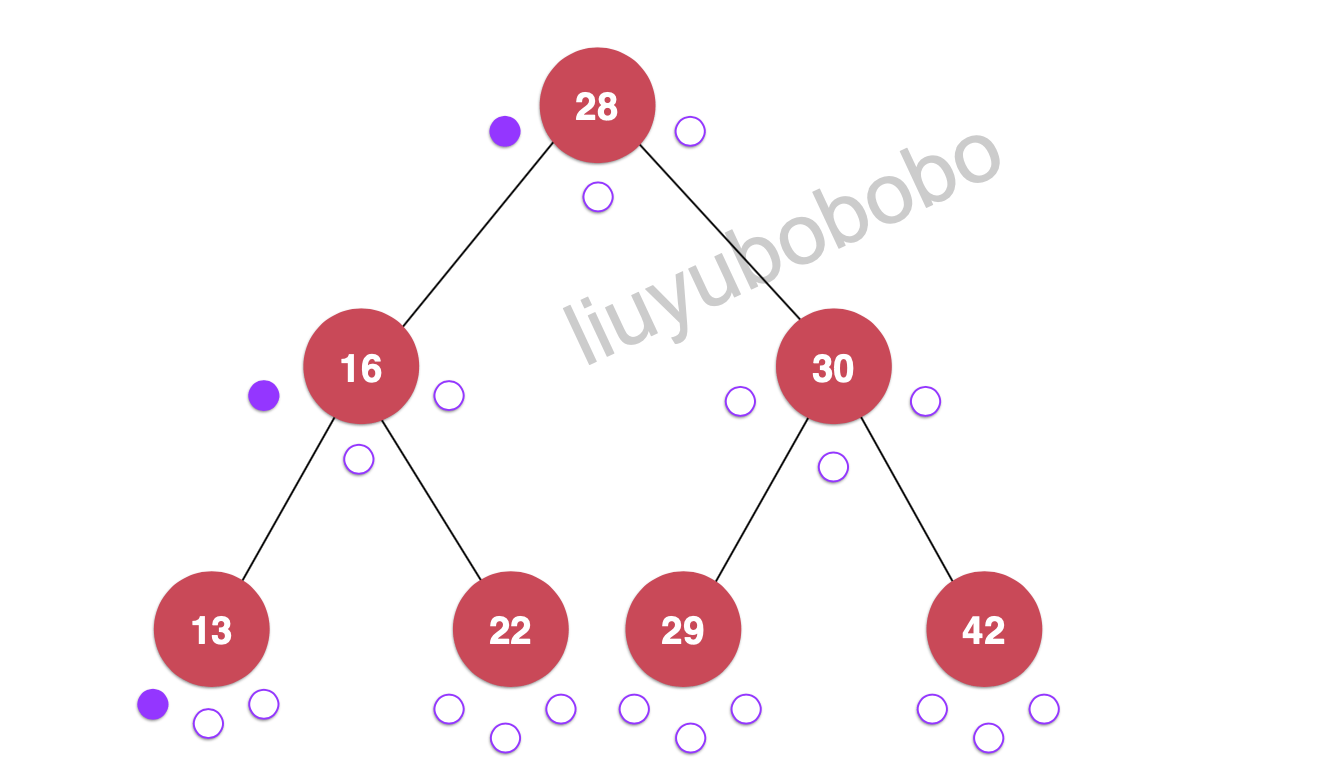
遍历:28, 16, 13
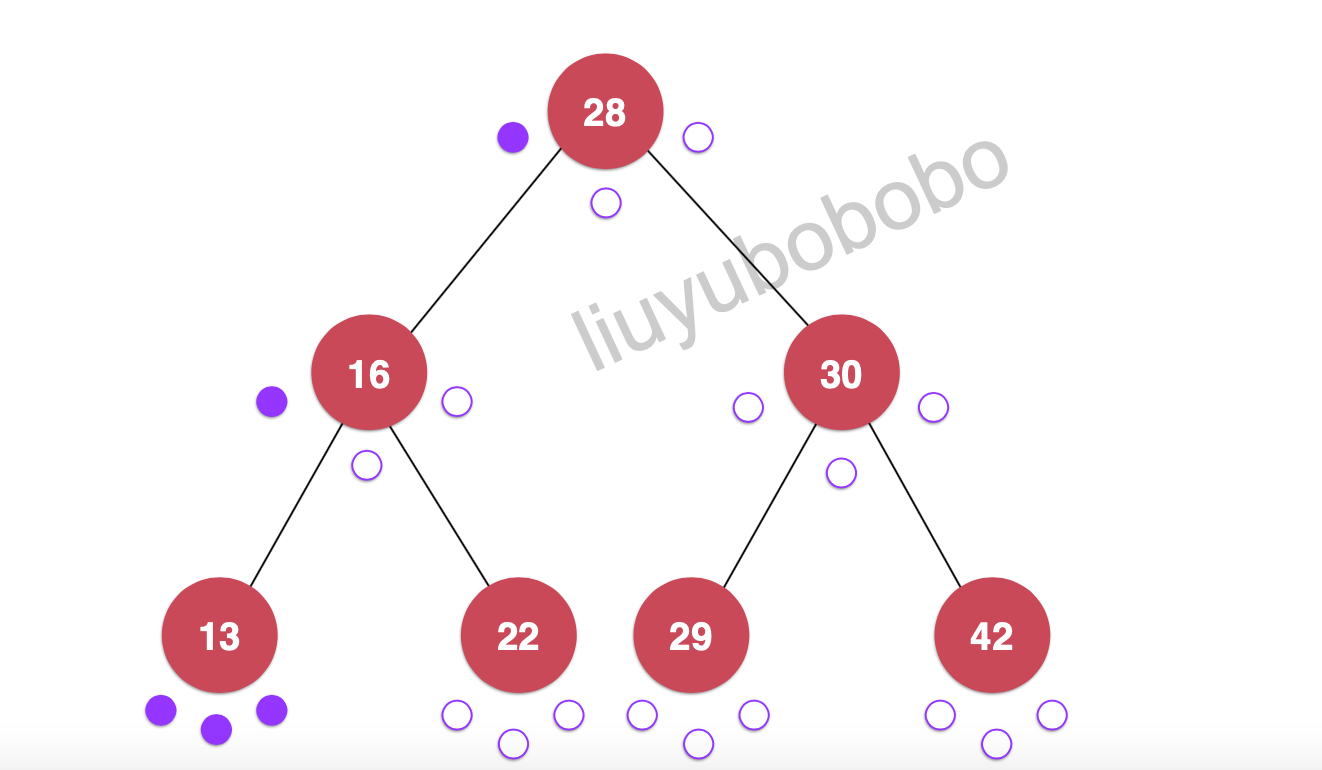
遍历:28, 16, 13
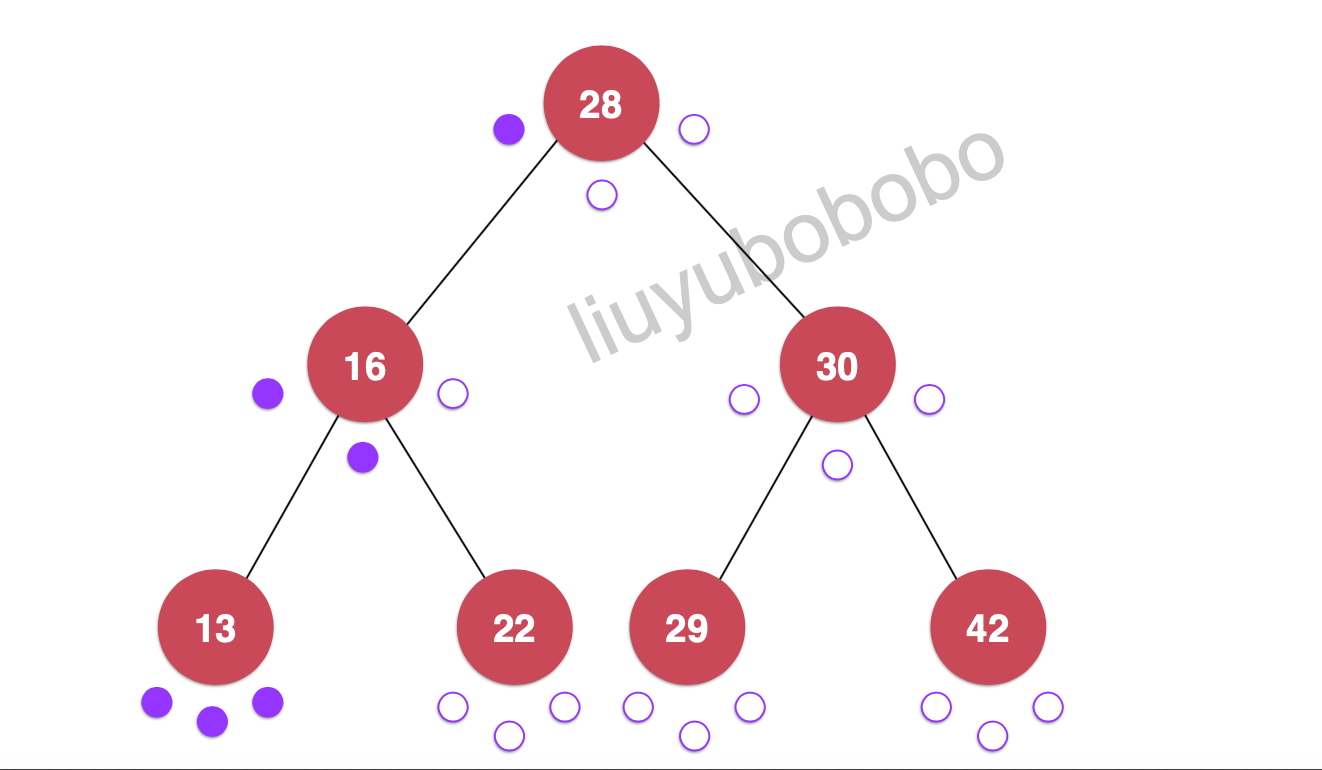
遍历:28, 16, 13, 22
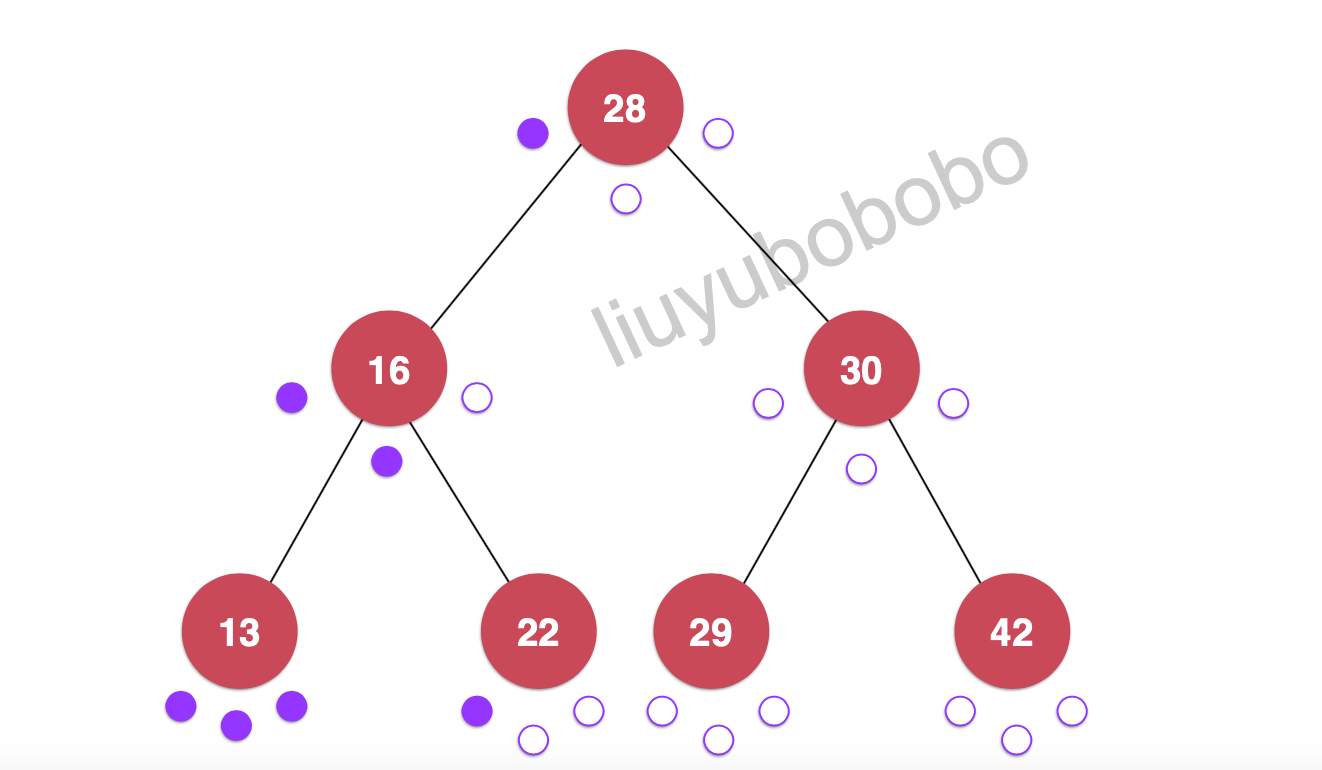
遍历:28, 16, 13, 22
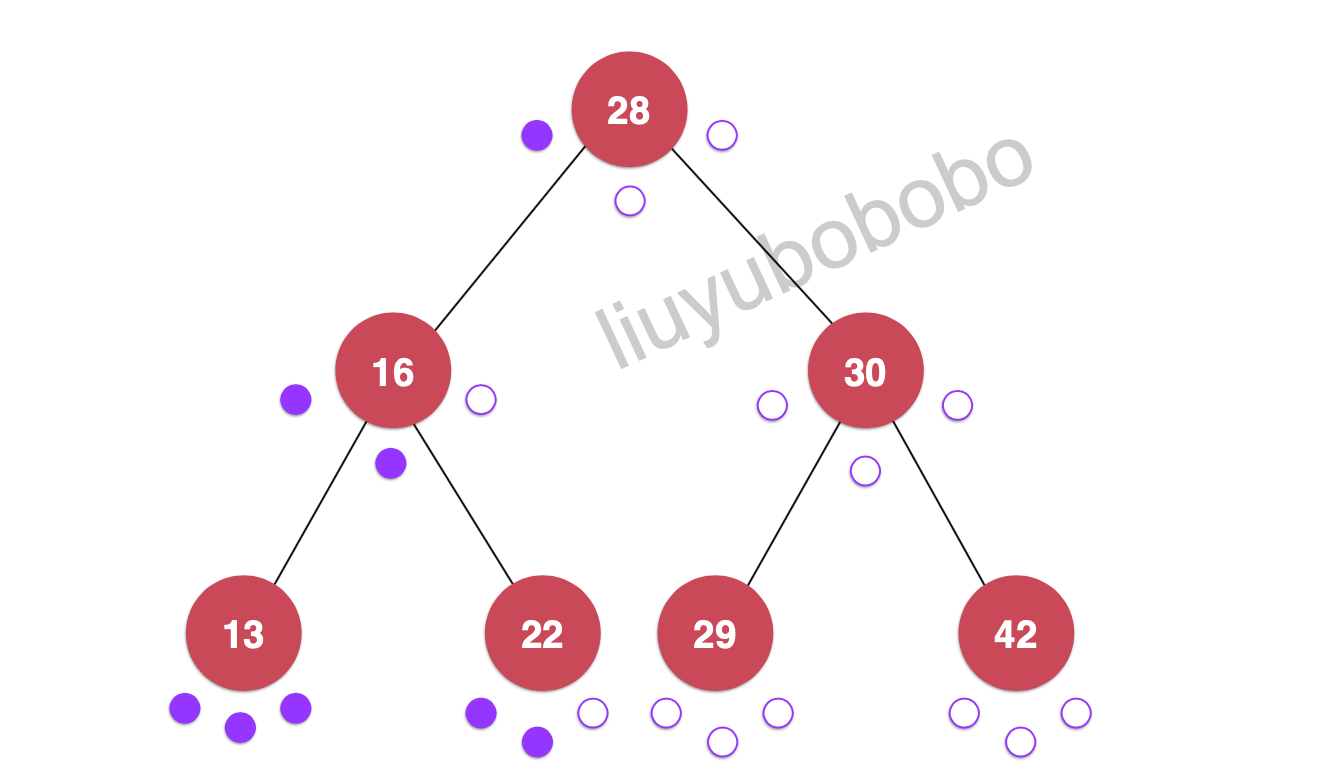
遍历:28, 16, 13, 22
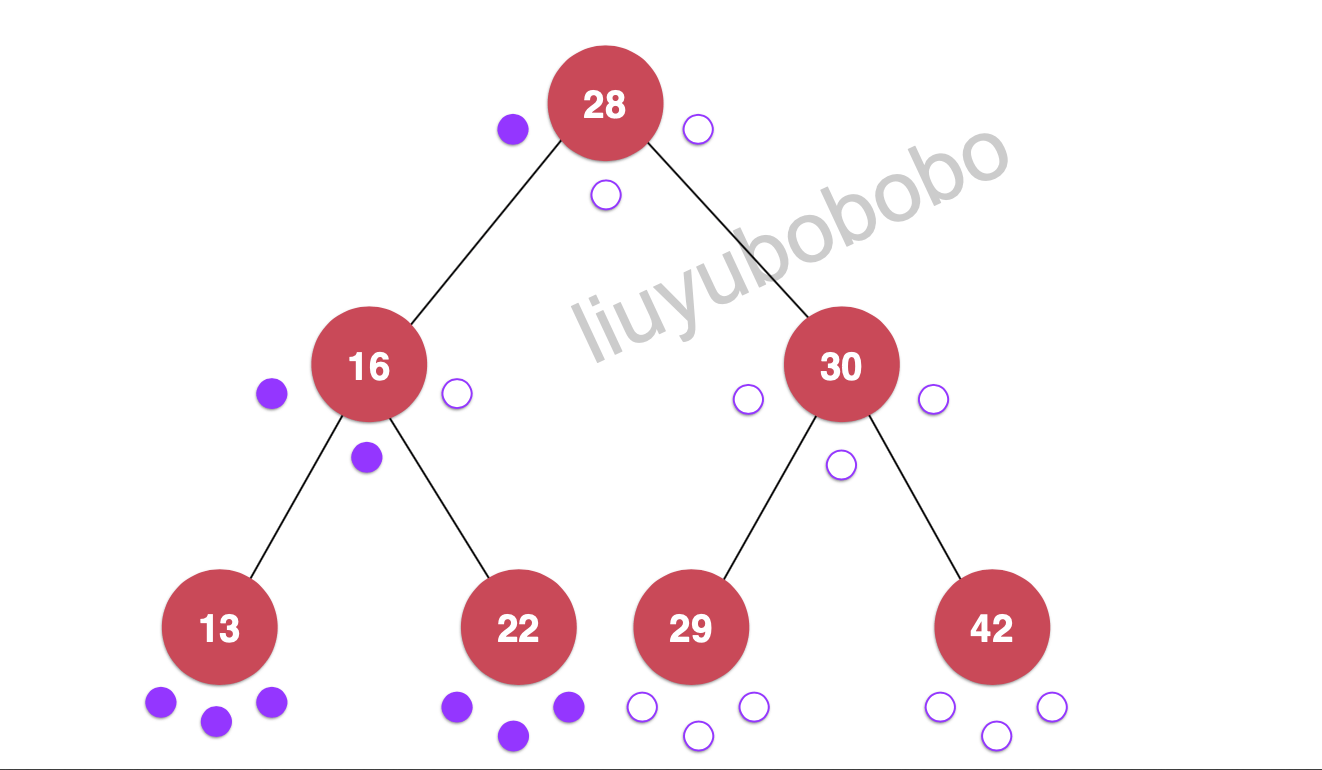
遍历:28, 16, 13, 22

依次类推 ……
最后完成整个前序遍历:
遍历:28, 16, 13, 22, 30, 29, 42
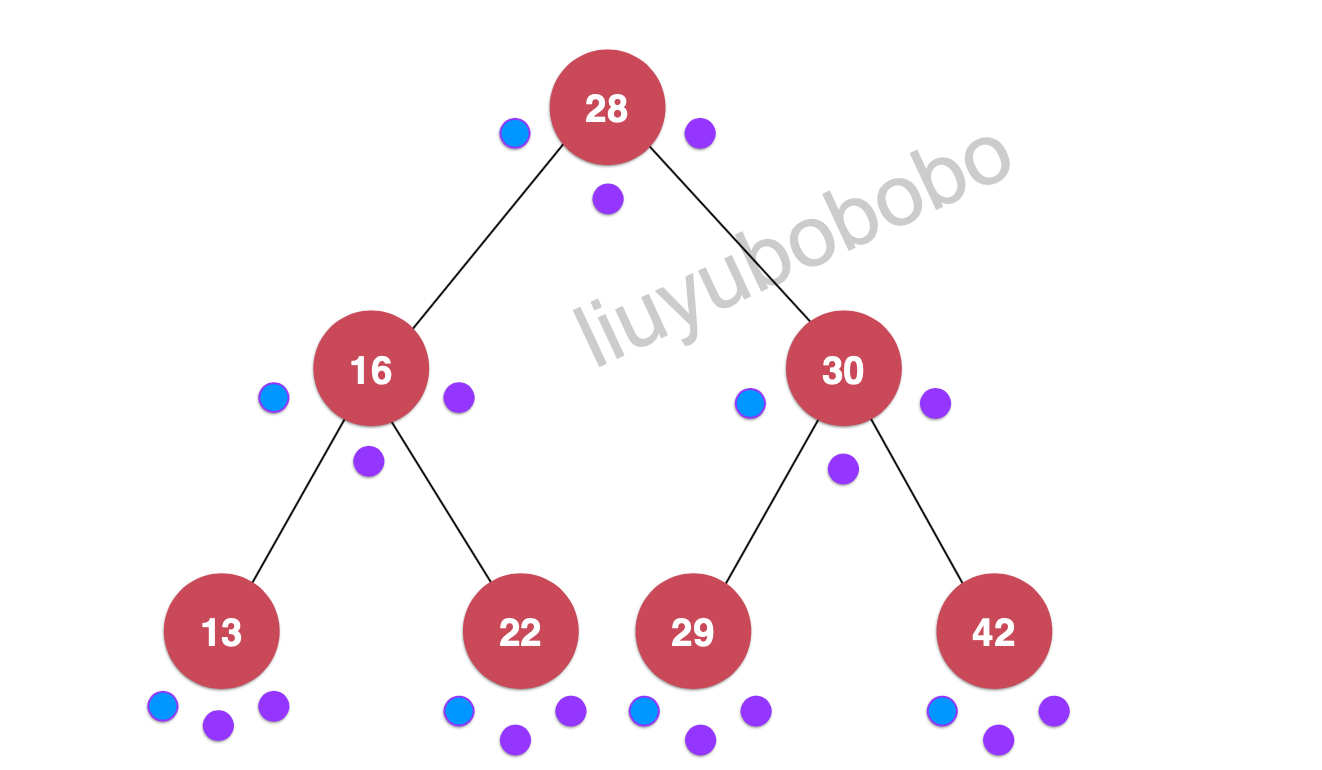
**代码实现(使用递归,c++实现) 在public中定义:
//前序遍历,传入节点,打印节点相应信息
void preOrder() {
return preOrder(root);
}
在private中定义:
//前序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void preOrder(Node *node) {
if (node != NULL) {
//不一定用打印,还可以对node->key和node->value进行操作
cout << node->key << endl;
preOrder(node->left);
preOrder(node->right);
}
}
中序遍历
按照前序遍历的模型和顺序,很容易看出中序遍历就是在中间点的时候进行遍历:(过程省略) 遍历:13, 16, 22, 28, 29, 30, 42 如下图:(可以看出由中序遍历可以看出遍历结果是有序的)
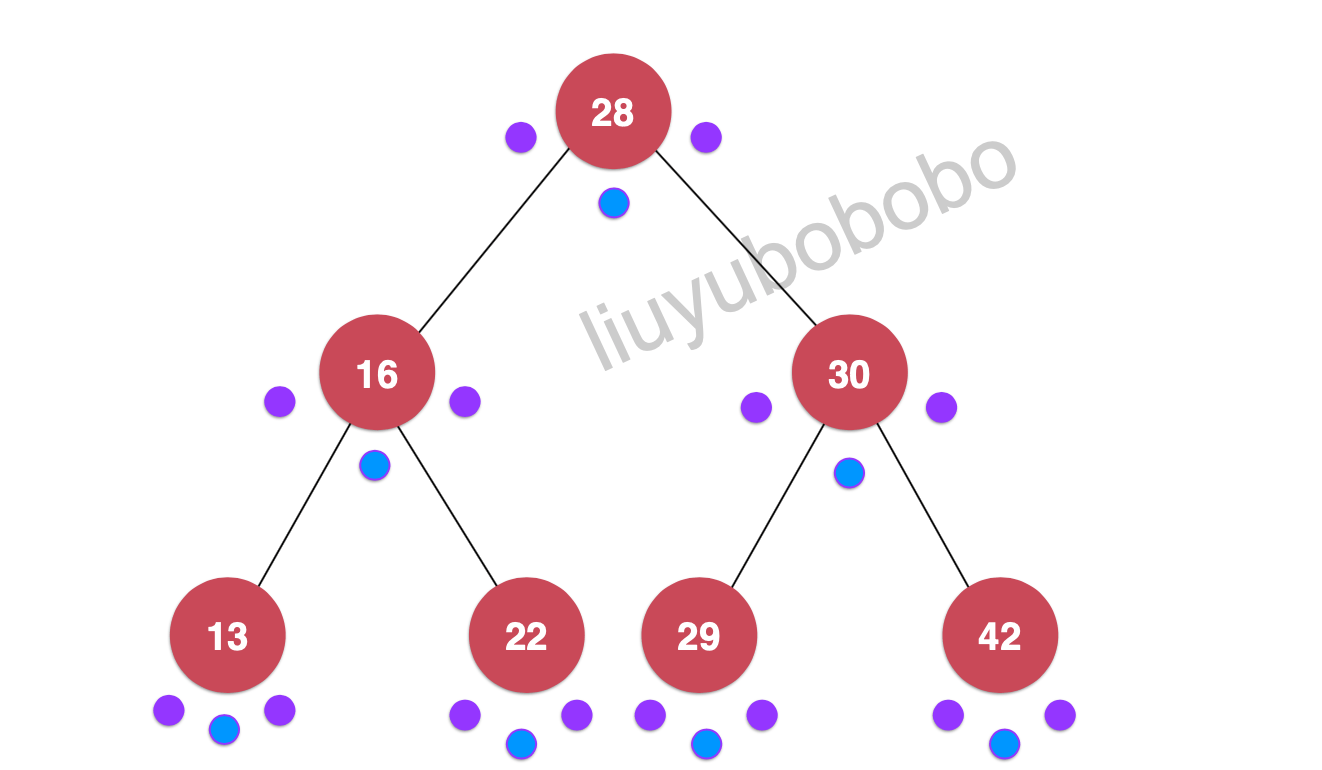 **代码实现(使用递归,c++实现)
在public中定义:
**代码实现(使用递归,c++实现)
在public中定义:
//中序遍历,以节点为node的节点为根节点
void inOrder() {
return inOrder(root);
}
在private中定义:
//中序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void inOrder(Node *node) {
if (node != NULL) {
inOrder(node->left);
cout << node->key << endl;
inOrder(node->right);
}
}
后序遍历
一样的逻辑,后序遍历就是在第三个点时进行遍历:(过程省略)
遍历:13, 22, 16, 29, 42, 30, 28
如下图:
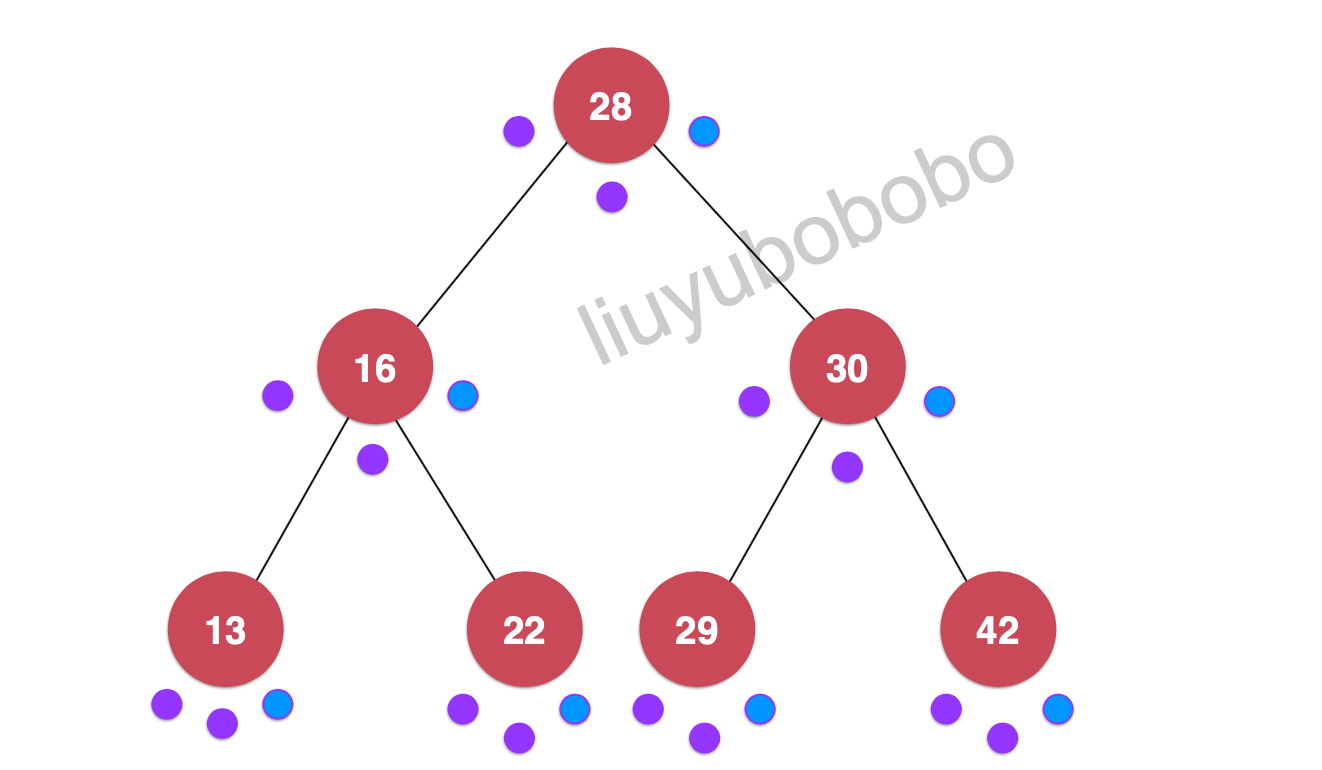 后序遍历有个重要的应用:二叉树的销毁(从子节点依次向上删除)
后序遍历有个重要的应用:二叉树的销毁(从子节点依次向上删除)
**代码实现(使用递归,c++实现) 在public中定义:
//后序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void postOrder() {
return postOrder(root);
}
在private中定义:
//后序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void postOrder(Node *node) {
if (node != NULL) {
postOrder(node->left);
postOrder(node->right);
cout << node->key << endl;
}
}
下面我们来使用后序遍历将二分搜索树销毁:
//析构函数的实现,其本质是后序遍历
void distroy(Node *node) {
if (node != NULL) {
distroy(node->left);
distroy(node->right);
delete node;
count--;
}
}
广度优先遍历
介绍
二分搜索树的广度优先(层序遍历),即逐层进行遍历,即将每层的节点存在队列当中,然后进行出队(取出节点)和入队(存入下一层的节点)的操作,以此达到遍历的目的。 通过引入一个队列来支撑层序遍历:
-
如果根节点为空,无可遍历;
-
如果根节点不为空:
-
先将根节点入队;
-
只要队列不为空:
-
出队队首节点,并遍历;
-
如果队首节点有左孩子,将左孩子入队;
-
如果队首节点有右孩子,将右孩子入队;
-
-
具体数据
以下图为例:
![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/ySF0wGBfpa.png!large)
- 我们使用一个队列——front 将28放入队列中
出:空
入:28
队列:28
遍历情况:空
![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/JNXew3g72P.png!large)
出:28
入:16, 30
队列:16, 30
遍历情况:28
![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/VPQQbBSdWo.png!large)
出:16
入:13 ,22
队列:30, 13, 22
遍历情况:28, 16
![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/CgS25HU8lU.png!large)
出:30
入:29 ,42
队列: 13, 22, 29, 42
遍历情况:28, 16, 30
![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/xqXqRSEH2L.png!large)
出:13
入:空
队列: 22, 29, 42
遍历情况:28, 16, 30, 13
![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/mVMQJoKlrQ.png!large)
出:22
入:空
队列: 29, 42
遍历情况:28, 16, 30, 13, 22
![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/b95bmIzhVU.png!large)
出:29
入:空
队列: 42
遍历情况:28, 16, 30, 13, 22, 29
![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/xEBErizheX.png!large)
出:42
入:空
队列: 空
遍历情况:28, 16, 30, 13, 22, 29, 42
![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/pxWszTUvAk.png!large)
遍历完成:
遍历情况:28, 16, 30, 13, 22, 29, 42
![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/UleaXFO3nX.png!large)
代码实现(使用递归,c++实现)
//层序遍历
void levelOrder(){
queue<Node*> q; //队列d
q.push(root); //将root入队
//队列不为空的情况
while(!q.empty()){
Node *node = q.front(); //将队列第一个元素取出
q.pop(); //是删除栈顶元素
cout<<node->key<<endl;
if(node->left)
q.push(node->left);
if(node->right)
q.push(node->right);
}
}
二分搜索树节点的删除(remove)
在这一小节中,我们会介绍二分搜索树中如何查找最小最大值、最小最大值的删除、删除任意节点(删除只有左孩子的节点、删除只有右孩子的节点和删除左右孩子都存在的节点);下面我们一一讲解:
查找最小最大值及其删除
查找最小最大值
其实很简单,首先我们想一想二分搜索树的定义就会明白,最小值在以跟节点的左孩子节点的左孩子节点………上,看图吧:
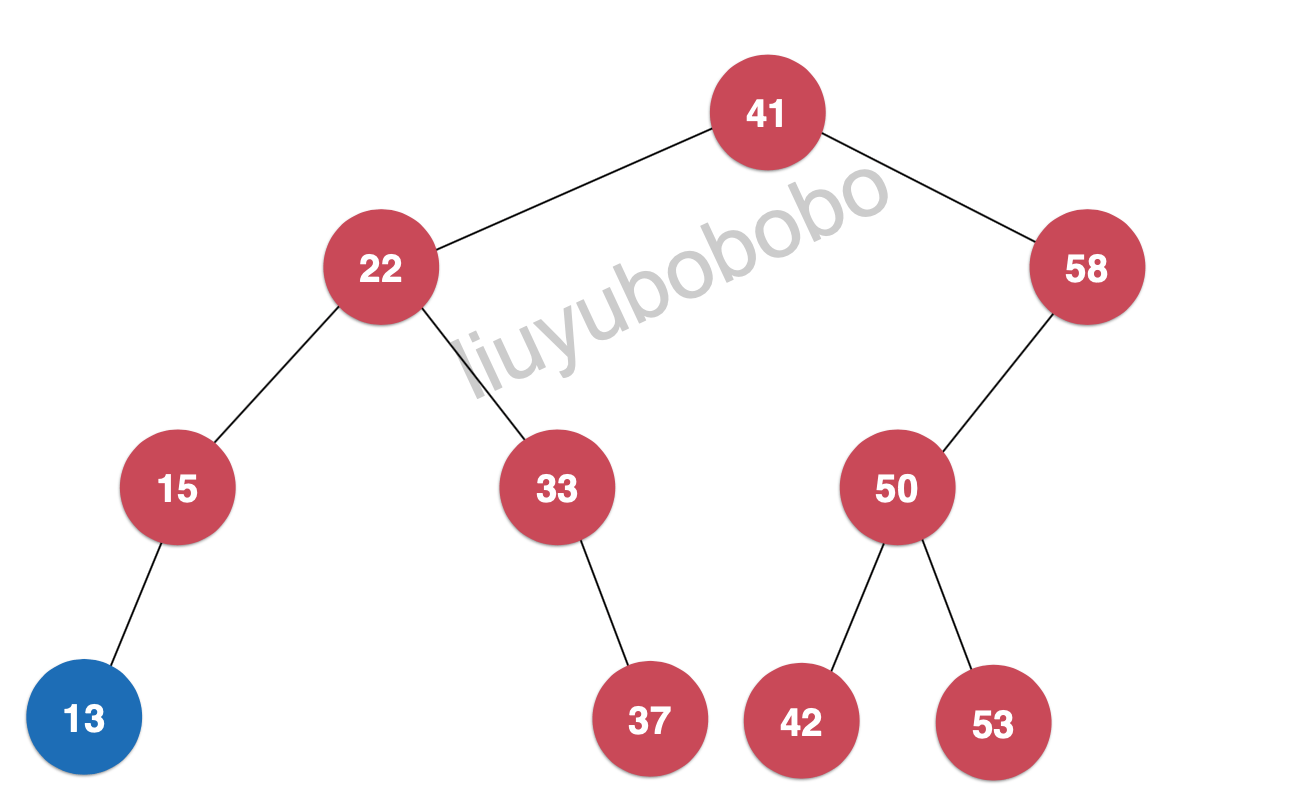
直接看代码吧! 在public中定义:
// 寻找二分搜索树的最小的键值
Node* minmum(){
assert(count != 0);
Node* minnode = minmum(root);
return minnode->left;
}
在private中定义:
// 寻找二分搜索树的最小的键值
Node* minmum(Node* node){
if(node != NULL){
minmum(node->left);
}
return node;
对于最大值嘛,逻辑一样的这里就省略了 直接上代码吧! 在public中定义:
// 寻找二分搜索树的最大的键值
Node* maxmum(){
assert(count != 0);
Node* maxnode = maxmum(root);
return maxnode ->right;
}
在private中定义:
// 寻找二分搜索树的最大的键值
Node* maxmum(Node* node){
if(node != NULL){
maxmum(node->right);
}
return node;
}
删除最小值最大值
以最大值为例:
其实就是将最大值找到,然后删除(
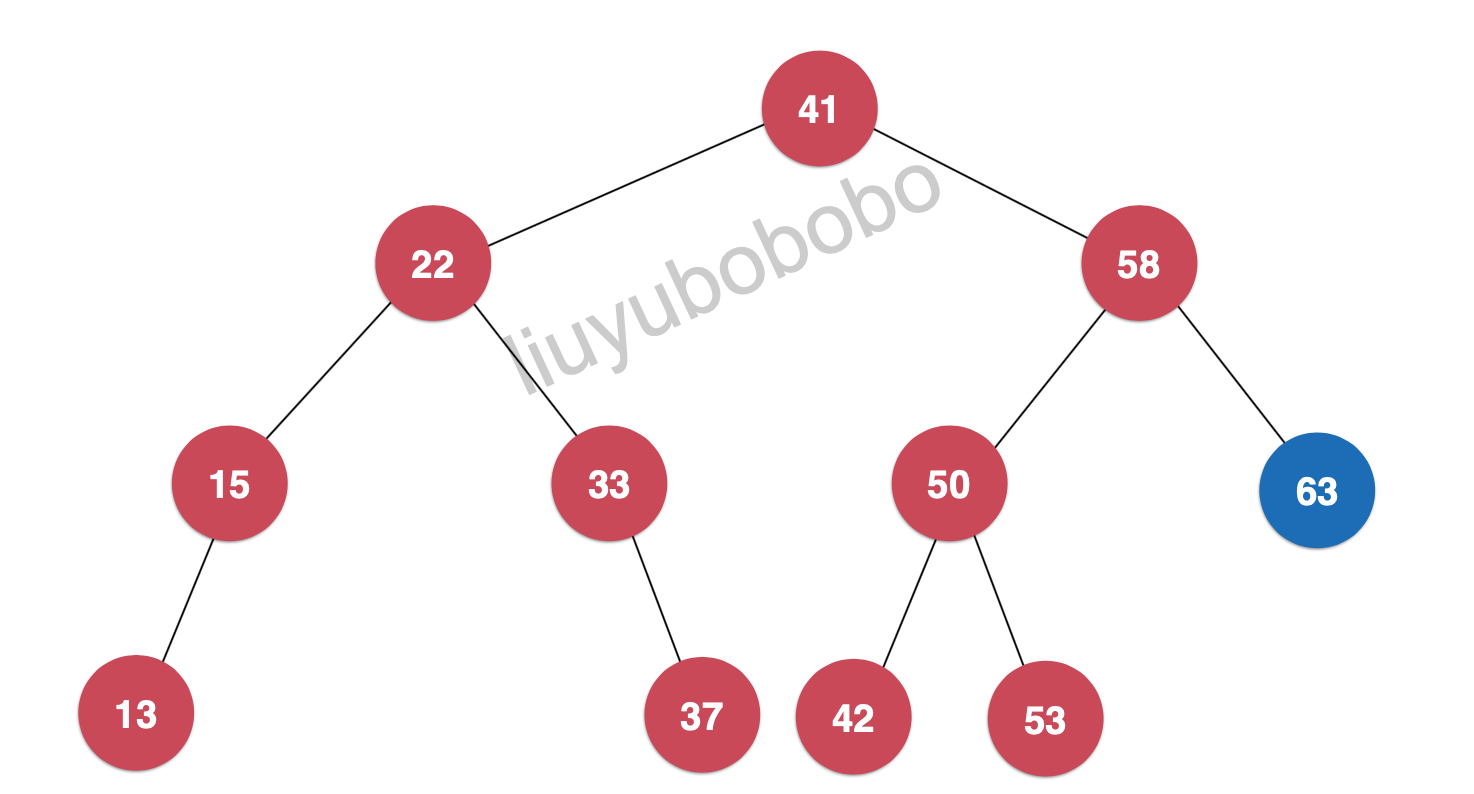
我们在public中定义:
//删除最大值的node
void removeMax(){
if(root){
root = removeMax(root);
}
}
在private中定义:
//从二分搜索树中删除最大值所在的节点
Node* removeMax(Node* node){
if(node->right == NULL){
Node* NODE = node->left;
delete node;
count--;
return NODE;
}
node->right = removeMax(node->right);
return node;
}
同理,删除最小值也就是将最小值查找到,然后删除: 我们依然在public中定义:
void removeMin(){
if(root){
root = removeMin(root);
}
}
在private中定义:
Node* removeMin(Node* node){
if(node->left == NULL){
Node* NODE = node->right;
delete node;
return NODE;
}
node->left = removeMin(node->left);
return node;
}
删除二分搜索树中任意节点
情况一
删除只有左孩子(右孩子)的节点
例如下图,我们删除节点58,但此时它存在左孩子,而从二分搜索树的定义可知如果将58删除,就应该将50节点作为41节点的右孩子节点;所以我们需要在删除58节点之前将50节点变成41节点的右孩子。
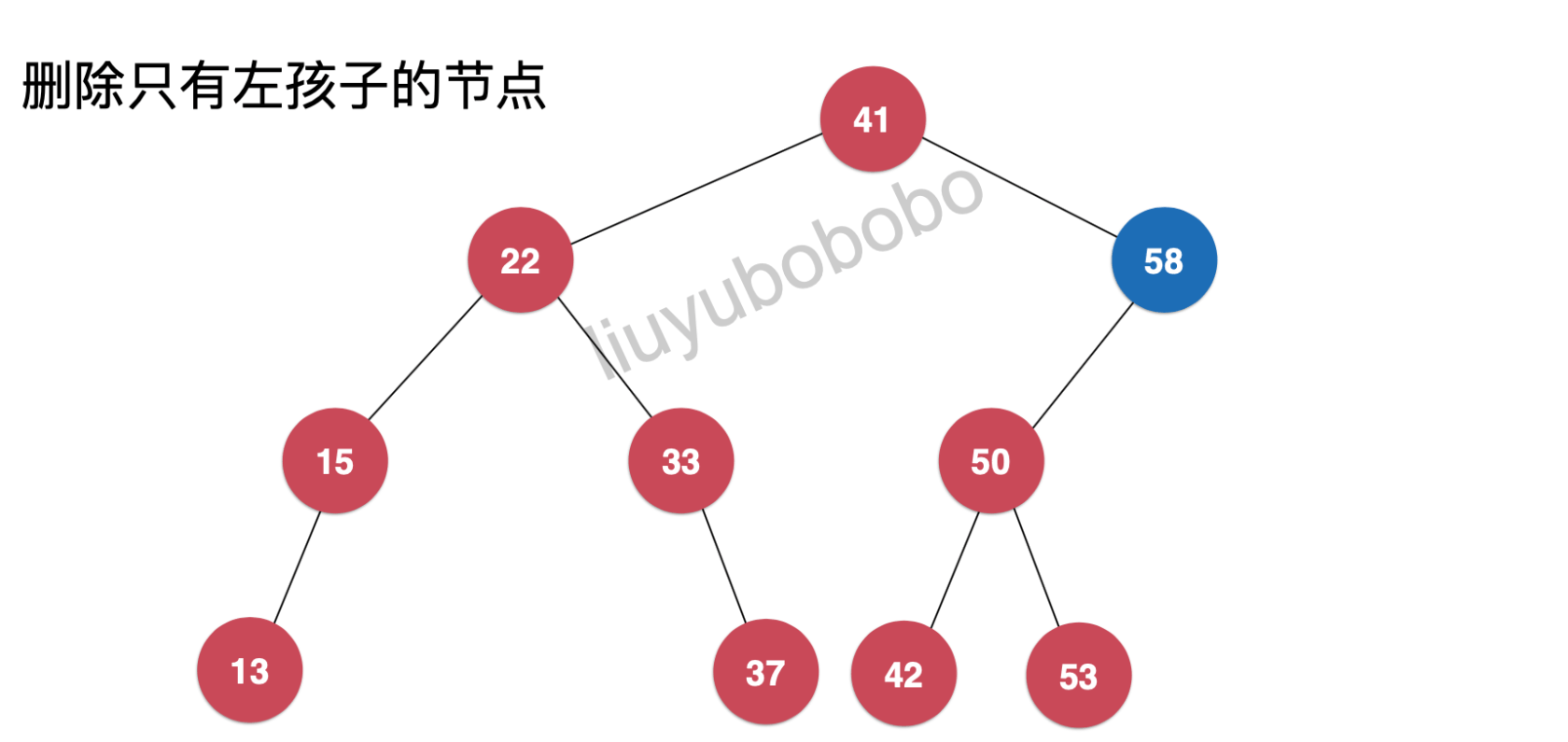 最后41节点的右子树应该变成:
最后41节点的右子树应该变成:
41
\
50
/ \
42 53
同理对于只有右孩子的节点是相同的逻辑(在这里省略) 下面看代码:(c++实现) 在public中定义:
//删除二分搜索树中值的任意节点
void remove( Key key){
root = remove(root, key);
}
在private中定义:
//删除二分搜索树中值的任意节点
Node* remove(Node* node, Key key){
//判断node是否为空
if(node == NULL) {
return NULL;
}
//先找到需要删除的值的node
else if(key < node->key) { //key为需要删除的,node->key为当前位置
node->left = remove(node->left, key);
return node;
}
else if(key > node->key) {
node->right = remove(node->right, key);
return node;
}
//这里就找到了需要delete的node
else { //key == node->key)
// 待删除节点左子树为空的情况
if(node->left == NULL){
Node* rightNode = node->right;
delete node;
count--;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node->right == NULL){
Node* leftNode = node->left;
delete node;
count--;
return leftNode;
}
}
情况二
删除同时拥有左右孩子的节点
如图,我们现在要删除图中58节点,如果直接删除58则41节点的右子树就不再是在该二分搜索树中了
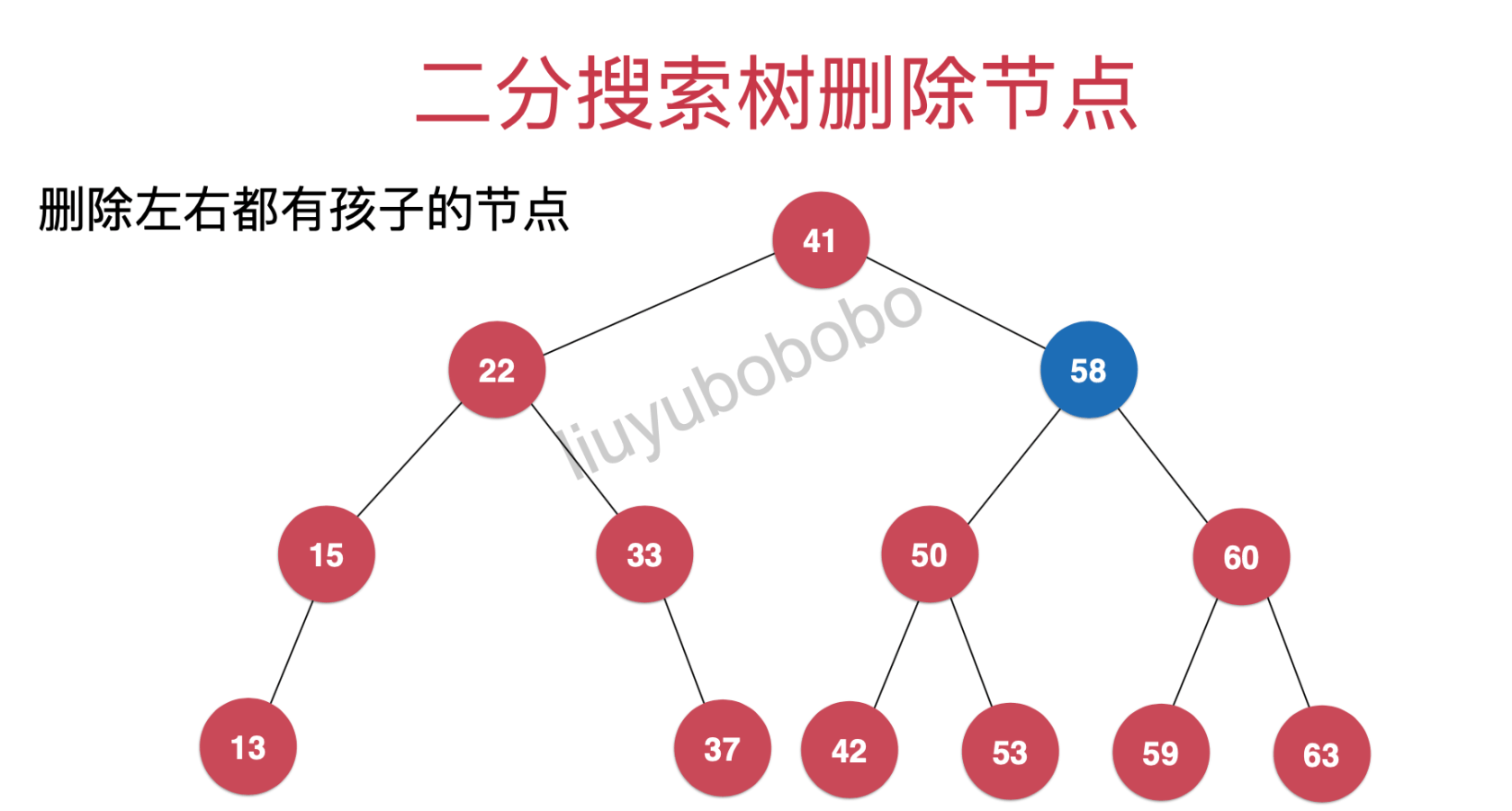
所以,现在我们需要将59拿出来,作为41节点的右孩子(这里只有59,53位置满足条件)
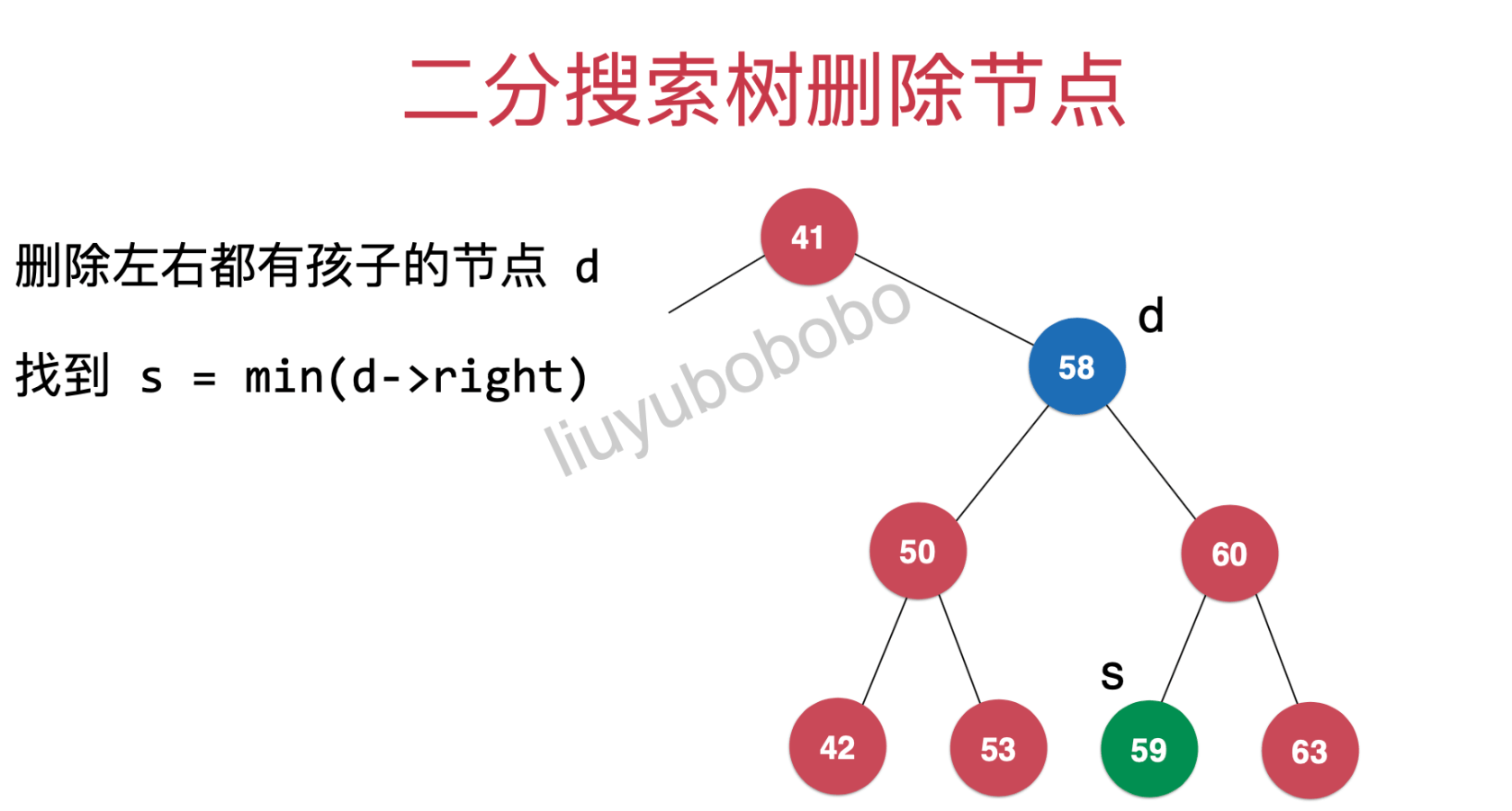 继续往下看:
继续往下看:
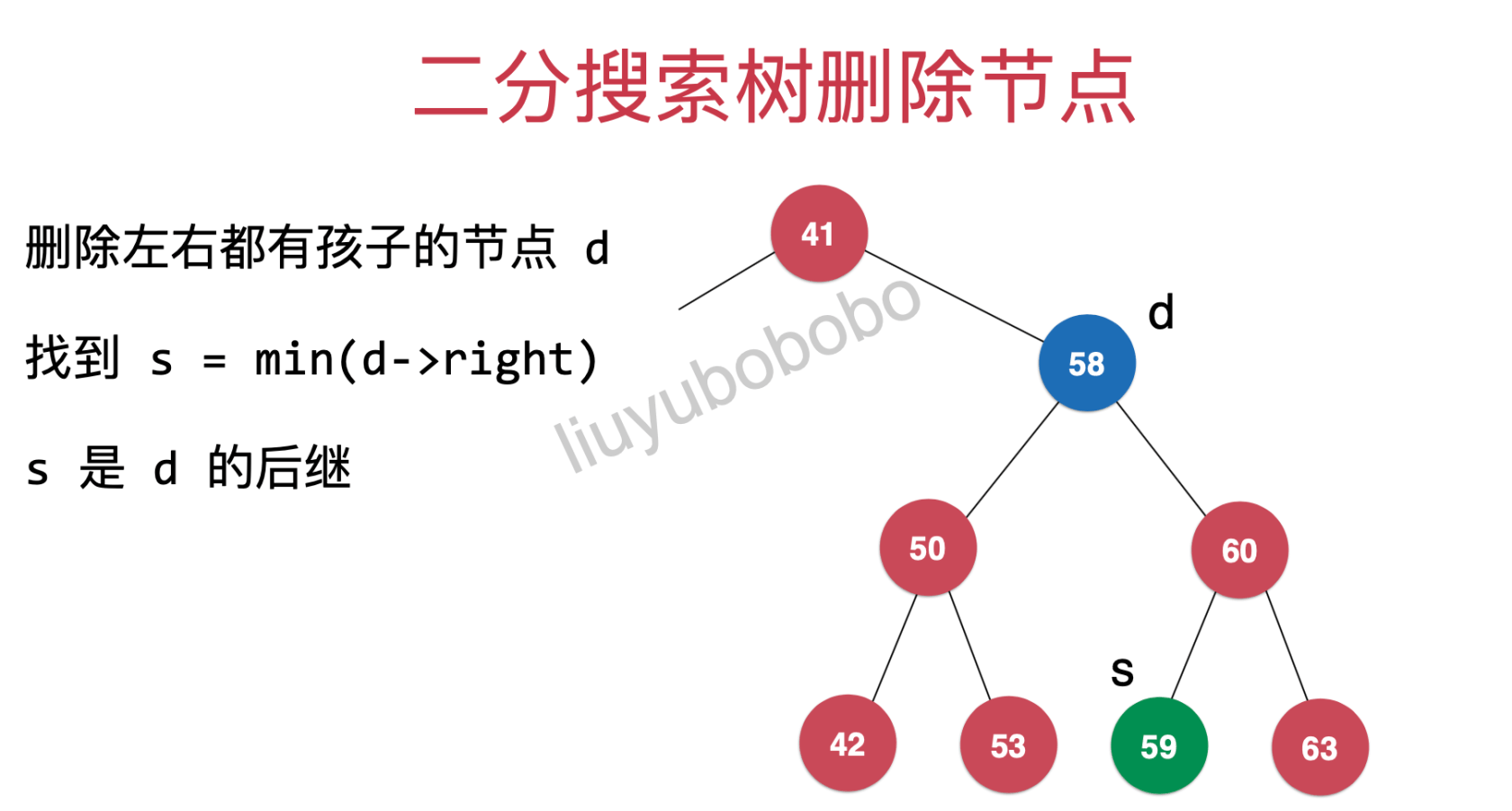 这里需要将原来58节点的右孩子变成59节点的右孩子
这里需要将原来58节点的右孩子变成59节点的右孩子
s->right = delMin(d->right)
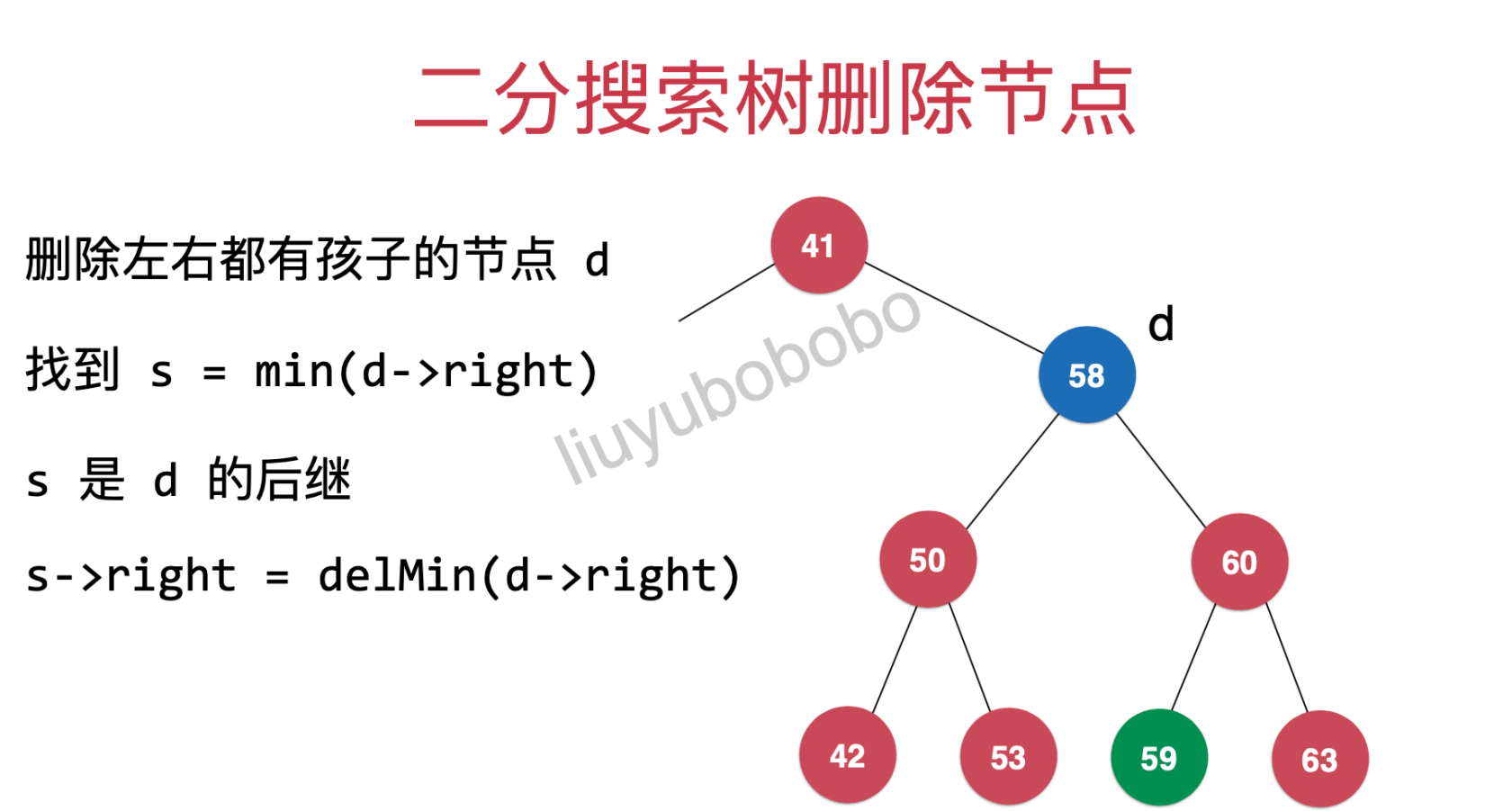
s->right = delMin(d->right)就变成了下图:
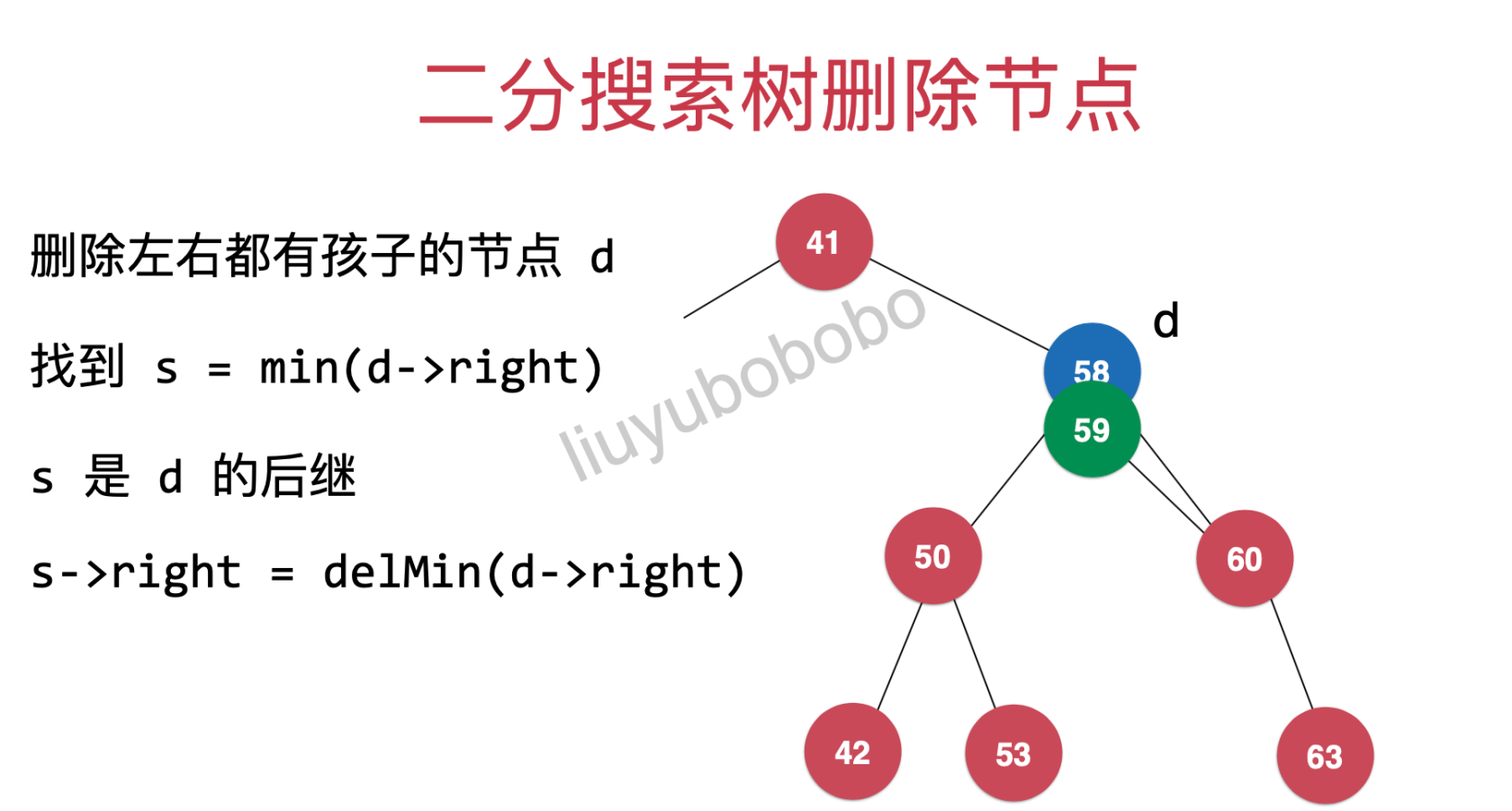
再将50节点变成59的左孩子
s->left = d->left:
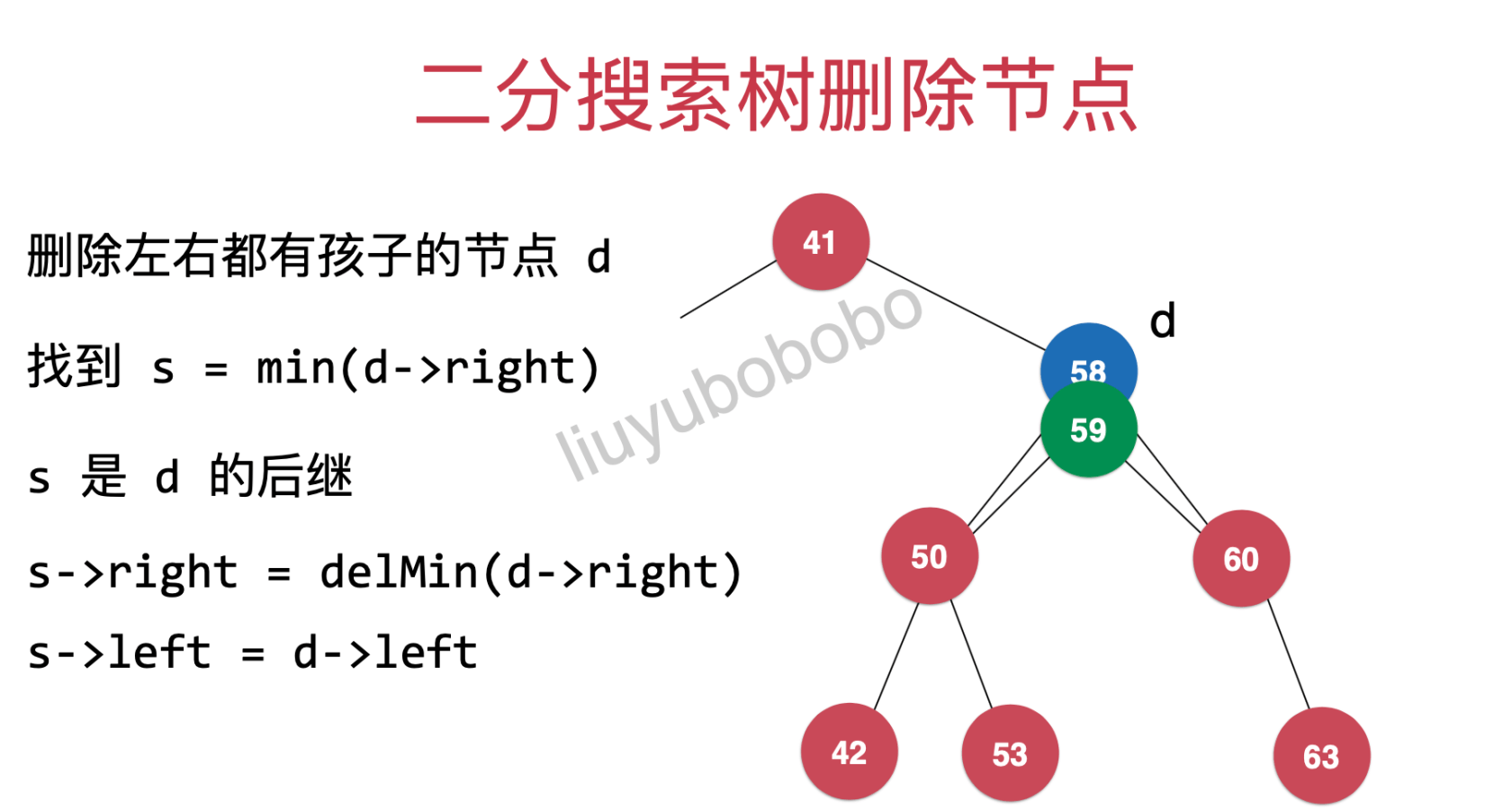
最后将58节点删除即可;利用递归将59节点返回给41节点(成为41节点的右孩子)。
下面看代码: 在public中定义:
//删除二分搜索树中值的任意节点
void remove( Key key){
root = remove(root, key);
}
在private中定义:
//删除二分搜索树中值的任意节点
Node* remove(Node* node, Key key){
//判断node是否为空
if(node == NULL) {
return NULL;
}
//先找到需要删除的值的node
else if(key < node->key) { //key为需要删除的,node->key为当前位置
node->left = remove(node->left, key);
return node;
}
else if(key > node->key) {
node->right = remove(node->right, key);
return node;
}
//这里就找到了需要delete的node
else { //key == node->key)
// 待删除节点左子树为空的情况
if(node->left == NULL){
Node* rightNode = node->right;
delete node;
count--;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node->right == NULL){
Node* leftNode = node->left;
delete node;
count--;
return leftNode;
}
// 待删除节点左右子树都不为为空的情况
Node *succeer =new Node(minmum(node->right)); //找到最小key值的节点返回给succeer
count ++;
succeer->right = removeMin(node->right); //将最小key值的node删除,并将返回值给succeer的右孩子
succeer->left = node->left;
delete node;
count--;
return succeer;
}
}
二分搜索树完整源代码
前面我们将了二分搜索树元素的插入、查找、遍历删除等,我将完整的源码放在这里了:
#include <iostream>
#include <queue>
#include <cassert>
using namespace std;
//套用模板函数
template <typename Key, typename Value>
class BST {
private:
//构造节点Node
struct Node {
Key key;
Value value;
Node *left;
Node *right;
Node(Key key, Value value) {
this->key = key;
this->value = value;
//初始值为空
this->left = this->right = NULL;
}
Node(Node *node){
this->key = node->key;
this->value = node->value;
this->left = node->left;
this->right = node->right;
}
};
//根节点
Node *root;
//节点数量
int count;
public:
BST() {
//初始值为空
root = NULL;
count = 0;
}
~BST() {
distroy(root);
}
int size() {
return count;
}
bool isEmpty() {
return count == 0;
}
//插入操作
void insert(Key key, Value value) {
//向根节点中插入key, value
root = insert(root, key, value);
}
//在树中寻找是否存在key
bool contain(Key key) {
return contain(root, key);
}
//找到key相应的节点并且返回value的地址
Node *seacher(Key key, Value value) {
return seacher(root, key, value);
}
//前序遍历,传入节点,打印节点相应信息
void preOrder() {
return preOrder(root);
}
//中序遍历,以节点为node的节点为根节点
void inOrder() {
return inOrder(root);
}
//后序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void postOrder() {
return postOrder(root);
}
//层序遍历
void levelOrder(){
queue<Node*> q;
q.push(root);
//队列不为空的情况
while(!q.empty()){
Node *node = q.front();
q.pop();
cout<<node->key<<endl;
if(node->left)
q.push(node->left);
if(node->right)
q.push(node->right);
}
}
// 寻找二分搜索树的最小的键值
Node* minmum(){
assert(count != 0);
Node* minnode = minmum(root);
return minnode->left;
}
// 寻找二分搜索树的最大的键值
Node* maxmum(){
assert(count != 0);
Node* maxnode = maxmum(root);
return maxnode ->right;
}
//删除最小值的node
void removeMin(){
if(root)
root = removeMin(root);
}
//删除最大值的node
void removeMax(){
if(root)
root = removeMax(root);
}
//删除二分搜索树中值的任意节点
void remove( Key key){
root = remove(root, key);
}
private:
//插入操作
//向以node为根节点的二分搜索树中,插入节点(key,value),使用递归算法 //返回插入新节点后的二分搜索树的根
Node *insert(Node *node, Key key, Value value) {
if (node == NULL) {
count++;
return new Node(key, value);
}
if (key == node->key) {
node->value = value;
}
else if (key > node->key) {
node->right = insert(node->right, key, value);
}
else //key < node->key
node->left = insert(node->left, key, value);
}
//在二分搜索树中查找key,存在返回trun不存在返回false
bool contain(Node *node, Key key) {
//元素不存在
if (key == NULL)
return false;
//元素存在
if (key == node->key)
return true;
else if (key > node->key)
return contain(node->right, key);
else return contain(node->left, key);
}
//在二分搜索树中找到相应元素并返回该元素的地址
Value *seacher(Node *node, Key key) {
if (key == NULL)
return NULL;
//找到key 返回value的地址
if (key == node->key)
return &(node->value);
else if (key > node->key)
return seacher(node->right, key);
else
return seacher(node->left, key);
}
//前序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void preOrder(Node *node) {
if (node != NULL) {
//不一定用打印,还可以对node->key和node->value进行操作
cout << node->key << endl;
preOrder(node->left);
preOrder(node->right);
}
}
//中序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void inOrder(Node *node) {
if (node != NULL) {
inOrder(node->left);
cout << node->key << endl;
inOrder(node->right);
}
}
//后序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void postOrder(Node *node) {
if (node != NULL) {
postOrder(node->left);
postOrder(node->right);
cout << node->key << endl;
}
}
//析构函数的实现,其本质是后序遍历
void distroy(Node *node) {
if (node != NULL) {
distroy(node->left);
distroy(node->right);
delete node;
count--;
}
}
// 寻找二分搜索树的最小的键值
Node* minmum(Node* node){
if(node != NULL){
minmum(node->left);
}
return node;
}
// 寻找二分搜索树的最大的键值
Node* maxmum(Node* node){
if(node != NULL){
maxmum(node->right);
}
return node;
}
// 从二分搜索树中删除最小值所在的节点
Node* removeMin(Node* node){
if(node->left == NULL){
Node* NODE = node->right;
delete node;
count--;
return NODE;
}
node->left = removeMax(node->left);
return node;
}
//从二分搜索树中删除最大值所在的节点
Node* removeMax(Node* node){
if(node->right == NULL){
Node* NODE = node->left;
delete node;
count--;
return NODE;
}
node->right = removeMax(node->right);
return node;
}
//删除二分搜索树中值的任意节点
Node* remove(Node* node, Key key){
//判断node是否为空
if(node == NULL) {
return NULL;
}
//先找到需要删除的值的node
else if(key < node->key) {
node->left = remove(node->left, key);
return node;
}
else if(key > node->key) {
node->right = remove(node->right, key);
return node;
}
//这里就找到了需要delete的node
else { //key == node->key)
// 待删除节点左子树为空的情况
if(node->left == NULL){
Node* rightNode = node->right;
delete node;
count--;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node->right == NULL){
Node* leftNode = node->left;
delete node;
count--;
return leftNode;
}
// 待删除节点左右子树都不为为空的情况
Node *succeer =new Node(minmum(node->right)); //找到最小key值的节点返回给succeer
count ++;
succeer->right = removeMin(node->right); //将最小key值的node删除,并将返回值给succeer的右孩子
succeer->left = node->left;
delete node;
count--;
return succeer;
}
}
};
void shuffle( int arr[], int n ){
srand( time(NULL) );
for( int i = n-1 ; i >= 0 ; i -- ){
int x = rand()%(i+1);
swap( arr[i] , arr[x] );
}
}
测试也写在这里了:
// 测试 remove
int main() {
srand(time(NULL));
BST<int,int> bst = BST<int,int>();
// 取n个取值范围在[0...n)的随机整数放进二分搜索树中
int n = 10000;
for( int i = 0 ; i < n ; i ++ ){
int key = rand()%n;
// 为了后续测试方便,这里value值取和key值一样
int value = key;
bst.insert(key,value);
}
// 注意, 由于随机生成的数据有重复, 所以bst中的数据数量大概率是小于n的
// order数组中存放[0...n)的所有元素 int order[n];
for( int i = 0 ; i < n ; i ++ )
order[i] = i;
// 打乱order数组的顺序
shuffle( order , n );
// 乱序删除[0...n)范围里的所有元素
for( int i = 0 ; i < n ; i ++ )
if( bst.contain( order[i] )){
bst.remove( order[i] );
cout<<"After remove "<<order[i]<<" size = "<<bst.size()<<endl;
}
// 最终整个二分搜索树应该为空
cout << bst.size() << endl;
return 0;
}
(图片来源:慕课网bobo老师)